
题目列表(包括答案和解析)
从近几年高考试题的革新看,有以下几个特点:(1)题量适当减少,尤其是选择题的个数在减少,今年北京卷的高考试题中调整为8个,但填空题由原来的4个增加至6个;(2)试卷结构更趋合理,通过改革题量及题型,既能更好地考查学生的知识水平,解题能力,又能给学生更多的思维时间和空间,更好地展现学生的思维水平;(3)试题的命制更具综合性与灵活性、新颖性,由于题量的减少,而又要考查的全面,就必然加强知识方法运用的综合性,这符合考试大纲中的“在知识网络的交汇处”命题的原则。此外,近几年的试题中加强了数学的应用意识(每年都会设置一道大的应用题),也在不断探索编制一些情境新颖,或能体现中等数学与高等数学的衔接的一些问题。
从试题的以上特点,不难得出我们的复习策略:
(1)不必猜题、押题,这样做无疑既耗费精力又容易造成复习的不全面;
(2)重视基础知识与方法的全面复习,争取以点带面;
(3)树立整张试卷一盘棋的思想意识,要获取最后的胜利,就需要全局考虑,争取“能得分处多得分,难得分处要争分”;
(4)考前的近半个月可做“温故”工作,即把一模,二模的试题重新检阅,以试题带动重点知识与方法的复习。
近些年的高考试题,对知识的考查既全面又突出重点,对课本中的重点知识与解题方法保持了较高的比例与深度,此外,在考查思维能力的同时,也兼顾考查学生的其他能力,如审题、分析能力,合理表述的能力,等等。常见的问题有:①审题不慎;②计算不准;③表述不当;④时间安排不合理。这些问题往往是导致失分的主要原因,不可不引起大家的重视。
高考试卷中重点考查的知识有哪些呢?不妨做一简略回顾。
考前查漏补缺
22、(Ⅰ)证明:
= ┈┈┈┈2分
┈┈┈┈2分
=
= ┈┈┈┈┈┈┈┈┈┈┈┈┈5分
┈┈┈┈┈┈┈┈┈┈┈┈┈5分
(Ⅱ)(1)在 个数
个数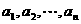 中,设正数之和为A,负数之和为B,则A+B=0,A-B=1,∴
中,设正数之和为A,负数之和为B,则A+B=0,A-B=1,∴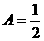 ,
, ,┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈7分
,┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈7分
所以, ,即
,即 ┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈9分
┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈9分
(2)由题意,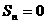 ,又由题(Ⅰ)知:
,又由题(Ⅰ)知: ┈┈11分
┈┈11分
 ,∴
,∴ ┈┈┈┈┈┈┈14分
┈┈┈┈┈┈┈14分
(2)证法2 设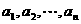 中,正数集为M,负数集为N,则
中,正数集为M,负数集为N,则 ┈┈┈┈┈┈┈11分
┈┈┈┈┈┈┈11分
又 ┈┈┈┈┈┈┈13分
┈┈┈┈┈┈┈13分
∴ ,即
,即 ┈┈┈┈┈┈┈14分
┈┈┈┈┈┈┈14分
21、(1)由 ,对其求导得:
,对其求导得: ,
,
设 ,则直线
,则直线 的斜率分别为
的斜率分别为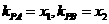 ,
,
∴直线 的方程为
的方程为 ,即
,即 ,
,
同理:直线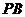 的方程为
的方程为 ,
,
∴可解得点 的坐标为
的坐标为 ,
,
又点 在准线
在准线 上,∴
上,∴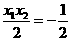 ,即
,即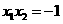 ,
,
∵ ,∴
,∴ ,猜想(1)成立。――――――――――4分
,猜想(1)成立。――――――――――4分
(另解:设 ,则点
,则点 在直线
在直线 上,∴
上,∴ ,∴
,∴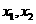 是方程
是方程 的两根,故
的两根,故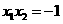 ,∴
,∴ ,∴
,∴ ,猜想(1)成立)
,猜想(1)成立)
(2)直线 的斜率
的斜率 ,
,
∴直线 的方程为
的方程为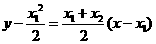 ,又
,又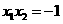 ,∴
,∴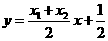 ,
,
显然直线 过焦点
过焦点 ,猜想(2)成立。―――――――――――――8分
,猜想(2)成立。―――――――――――――8分
(3) ,
, ,
,
∴

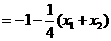 ,
,
又 ,
,
∴ ,
,
所以 恒成立,
恒成立, 为常数
为常数 。―――――――――――――――12分
。―――――――――――――――12分
20、解:∵ ,∴
,∴
又 , ∴
, ∴ ,
,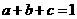 ,∴
,∴
∴ ―――――――――――――――――――――――――4分
―――――――――――――――――――――――――4分
(2)∵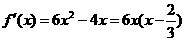 ,∴当
,∴当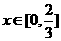 时,
时, ,
,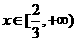 时,
时, ,∴
,∴ 在
在 上单调减,在
上单调减,在 上单调增。――――――――6分
上单调增。――――――――6分
又∵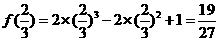 ,所以
,所以
①当 时,
时, 在
在 上单调减,故
上单调减,故
 ,故
,故 不合题意―――――――――――――――――――――――――――9分
不合题意―――――――――――――――――――――――――――9分
②当 时,
时,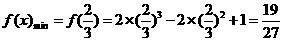 ,适合题意。
,适合题意。
综上可得,实数 的取值范围为:
的取值范围为: ―――――――――――――――――12分
―――――――――――――――――12分
19、(1)取AC中点D连A1D,则易知A1D 底面
底面 ,取AB中点E,连
,取AB中点E,连 ,可得DE//BC且DE
,可得DE//BC且DE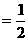 BC,∴DE⊥AB,由三垂线定理可得A1E⊥AB,∴∠A1ED为侧面A1ABB1与底面ABC的所成二面角的平面角
BC,∴DE⊥AB,由三垂线定理可得A1E⊥AB,∴∠A1ED为侧面A1ABB1与底面ABC的所成二面角的平面角
∵A1D= DE=1 ∴∠A1ED=60°,面A1ABB1与底面ABC的所成二面角为60°―4分
DE=1 ∴∠A1ED=60°,面A1ABB1与底面ABC的所成二面角为60°―4分
(2)设C到侧面A1ABB1的距离为h,∵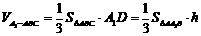
又∵
即顶点C到侧面A1ABB1的距离为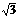 .-8分
.-8分
(3)取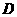 点为坐标原点,过
点为坐标原点,过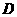 点垂直于
点垂直于 的直线为
的直线为 轴,
轴, 为
为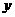 轴,
轴, 为
为 轴建立空间直角坐标系。易得:
轴建立空间直角坐标系。易得: 、
、 、
、 、
、 ,∴
,∴ ,
, ,
,
∴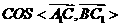


∴异面直线 与
与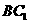 所成的角为
所成的角为 ――――――――――――――12分
――――――――――――――12分
18、解:(1)记“一次取出3条鱼,其中两种鱼均出现”为事件A,――――――――2分
则 ――――――――――――――――――――――6分
――――――――――――――――――――――6分
(2)记“每次取出鱼后放回,在三次取鱼中,第二次、第三次均取到鲤鱼”为事件B,“每次取出鱼后放回,第一次取到鲫鱼,第二次、第三次均取到鲤鱼”为事件B1,“每次取出鱼后放回,三次均取到鲤鱼”为事件B2,则 ,
,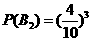 -10分
-10分
∴ ―――――――――――――――――――12分
―――――――――――――――――――12分
17、解:(1) =(2-2sinA,cosA+sinA),
=(2-2sinA,cosA+sinA), =(sinA-cosA,1+sinA),
=(sinA-cosA,1+sinA),
∵ //
// ∴(2-2sinA)(1+sinA)-(cosA+sinA)(sinA-cosA)=0;―――――2分
∴(2-2sinA)(1+sinA)-(cosA+sinA)(sinA-cosA)=0;―――――2分
化简得: ―――――――――――――――――――――――――3分
―――――――――――――――――――――――――3分
∵△ABC为锐角三角形,sinA=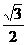 ∴A=60° ――――――――――――――6分
∴A=60° ――――――――――――――6分
(2)y=2sin2B+cos( )=2sin2B+cos(
)=2sin2B+cos( )=2sin2B+cos(2B-60°)
)=2sin2B+cos(2B-60°)
=1-cos2B+cos(2B-60°) =1+sin(2B-30°)―――――――――――――――10分
当B=60°时取最大值2―――――――――――――――――――――――――12分
22.(14分)设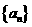 、
、 为两个数列,记
为两个数列,记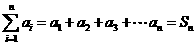 (
( )
)
(1)求证:
(2)设数列 满足
满足 ,
, ,①求证:
,①求证: ,(
,(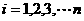 );
);
②
高考适应性考试
数学试卷评分标准
21.(12分)已知抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,过
,过 上一点
上一点 作抛物线的两条切线,切点分别为
作抛物线的两条切线,切点分别为 ,现某学习小组在研究讨论中提出如下三个猜想:
,现某学习小组在研究讨论中提出如下三个猜想:
(1)直线 恒成立;
恒成立;
(2)直线 恒过定点
恒过定点 ;
;
(3)等式 中的
中的 恒为常数。请你一一进行验证。
恒为常数。请你一一进行验证。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com