
题目列表(包括答案和解析)
2. 设集合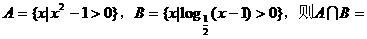 ( )
( )
A. 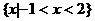 B.
B. 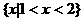 C.
C. 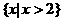 D.
D. 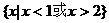
1. 平面直角坐标系中,两点A(cos80°,sin80°),B(cos20°,sin20°),则|AB|=( )
A. 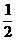 B.
B.
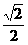 C.
C. 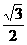 D. 1
D. 1
(八)排列组合:两个原理(加法原理、乘法原理)的应用。
[典型例题]
例1. 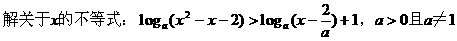
分析与解:
显然,这是解对数不等式,方法是化为同底型对数不等式,需要注意的是勿忘“真数>0”。解题时,建议运用等价转化的格式,以使得解题步骤清晰、明朗、简捷;此外,由于要运用对数函数单调性转化不等式,故还需对底数a分类讨论,但不宜太早地分类。
解: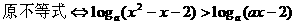
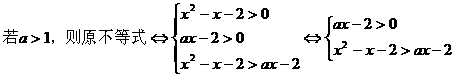



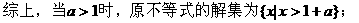
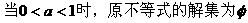
注:解不等式需熟练掌握,它是研究其他问题的重要工具,如求函数定义域、值域,求参数的取值范围等等,也是高考的重点考查内容。
例2. △ABC中,角A、B、C的对边分别为a,b,c,且满足

(I)求角B的度数;

分析与解:
(I)已知等式中含有角A、B、C,所求者为角B,故需把角A、C用B表示出来,转化为只含角B的三角方程,由此可求得角B。
(II)已知a+c=3,欲求a,c,只需再建立一个以a、c为未知数的方程,然后与a+c=3联立,既可求a,b的值,注意到由(I)可知角B大小,由余弦定理,可得到a,c的方程。
解:
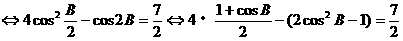

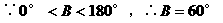
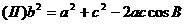
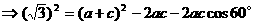
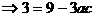
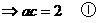

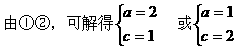
注:对三角恒等变形能力的考查通常与解三角形相综合,一方面体现了三角恒等变形的工具性,另一方面,也体现了知识的综合性,需熟练掌握,此外,对三角形恒等变形能力的考查,往往也结合三角函数的性质。例如:
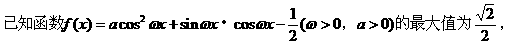
其最小正周期为π。
(I)求实数a,ω的值;
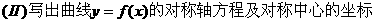
答案:(I)a=1,ω=1;

例3. 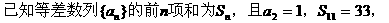
(I)求{an}的通项公式;

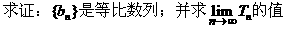
分析与解:
这是一道有关数列的基本题,已知条件明确指明{an}是等差数列,欲求其通项公式,只需由a2=1及S11=33,解出首项a1及公差d即可;而欲证{bn}是等比数列,只需根据等比

解:(I)设{an}公差为d,首项为a1,则
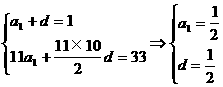

(II)对任意自然数n,

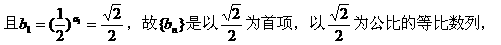
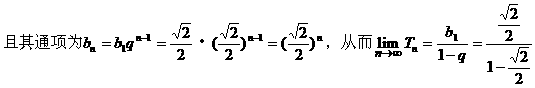
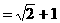
注:本题不难,但却考查了有关数列的若干重要概念、公式,在考前的复习中,应再多做些此类习题,提高解题的速度与准确。此外,对数列的考查还经常以递推公式为背景考查归纳、探索能力,也常常把数列与函数知识综合考查。
例如:

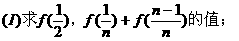
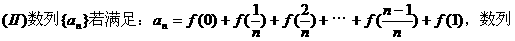
{an}是否为等差数列?请对你的结论给予证明。
答案: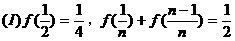
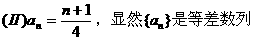
例4. 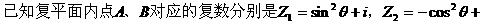

(I)求复数Z;
(II)指出点B的轨迹;

分析与解:
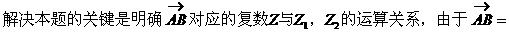
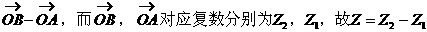
解: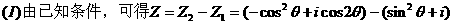

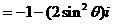

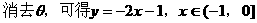
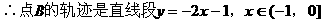

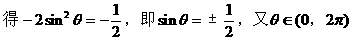

注:复数的运算是高考考查的重点,其几何意义则是另一重点,需正确理解,复数与复平面内点之间的对应关系,复数与向量的对应关系,以及向量的加减运算法则--平行四边形法则及三角形法则。
例5. 如图,棱长为1的正方形ABCD-A1B1C1D1中,E是CC1的中点,
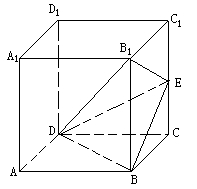
(I)求证:平面B1DE⊥平面B1BD;
(II)求二面角B-B1E-D的余弦值;
(III)求点B1到平面BDE的距离。
分析:(I)欲证平面B1DE⊥平面B1BD,就需根据面面垂直的判定定理,先证线面垂直,尝试发现,图中已有直线皆不合要求,需添加此直线,注意到EB1=ED(等腰三角形),取B1D中点M,则EM⊥B1D,再继证EM⊥BD即可。
(II)由(I)之证明及三垂线定理,可构造二面角的平面角。
(III)点B1到平面BDE的距离可看作三棱锥B1-BDE的面BDE上的高,只需利用“等体积法”求该距离。
(I)证明:取B1D的中点M,连结EM
∵△EB1D中,EB1=ED,∴△EB1D为等腰三角形
∴EM⊥B1D,注意到点M也是AC1的中点,
△C1AC中,E、M分别为两边C1C,C1A的中点,
∴EM∥AC,又AC⊥BD
∴EM⊥BD,
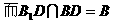
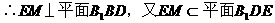
∴平面B1DE⊥平面B1BD。
(II)由(I)的结论,若过B作BN⊥DB1于N,则得BN⊥平面B1ED,
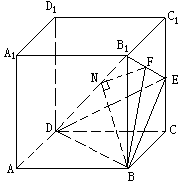
过N作NF⊥B1E于F,连结BF,由三垂线定理,BF⊥B1E,
∴∠BFN是二面角B-B1E-D的平面角,
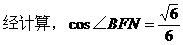
(III)设B1到平面BDE的距离为d,
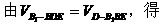


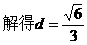
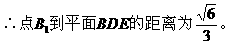
例6. 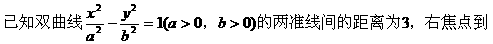

(I)求双曲线方程;
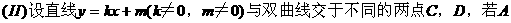
点坐标为(0,-1)且|AC|=|AD|,求k的取值范围。
分析:(I)要确定双曲线方程,需待定方程中的a2,b2,只需由已知条件列出关于a2,b2的两个方程即可。

弦,若CD中点为P,则易得AP⊥CD,从而可联想到kAP·kCD=-1以及中点坐标公式……
解:(I)设双曲线右焦点为(c,0),(c>0),
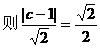


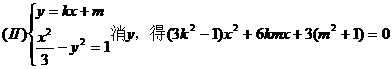
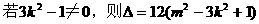
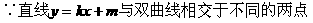

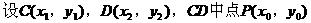
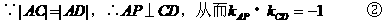
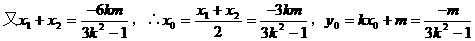
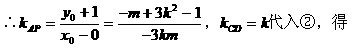
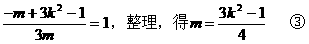
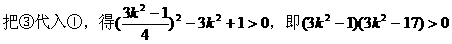
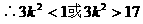
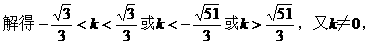
[模拟试题]
(七)解析几何:直线方程(包括斜率、倾斜角),点到直线的距离,圆锥曲线的方程、性质,直线与圆锥曲线的位置关系,参数方程与极坐标方程(掌握互化公式是解此类题的通法)
(六)立体几何:有关直线、平面的位置关系的定理(要熟练),证明直线与平面的平行与垂直,计算空间的角(异面直线成角、线面角、二面角)与距离(点线、点面、线面、面面距离),以及计算多面体或旋转体的表面积、体积。
(五)复数:基本的运算、加减法的几何意义。
(四)三角:正、余弦定理,三角恒等变形、(公式熟、准)、三角函数图象性质、解三角形。
(三)数列:两种基本数列(等差数列与等比数列),递推关系式、极限、数学归纳法证明、求和。
(二)不等式:解不等式、证明不等式(常用比较法、数学归纳法)
(一)函数:定义域、值域、解析式、判断或证明函数的单调性、奇偶性、反函数、最值、图象。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com