
题目列表(包括答案和解析)
4.下列函数中,值域是R+的是( )
(A)y= (B)y=2x+3 x
(B)y=2x+3 x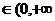 )
)
(C)y=x2+x+1
(D)y=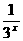
3.若函数y=f(x)的定义域是[2,4],y=f(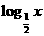 )的定义域是( )
)的定义域是( )
(A)[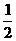 ,1] (B)[4,16] (C)[
,1] (B)[4,16] (C)[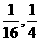 ] (D)[2,4]
] (D)[2,4]
2.如图,U是全集,M、P、S是U的三个子集,则阴影部分所表示的集合是( )
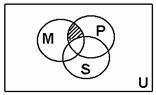 (A)(M
(A)(M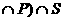 (B)(M
(B)(M
(C)(M P)
P) (CUS)
(D)(M
(CUS)
(D)(M P)
P)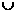 (CUS)
(CUS)
1.设A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},满足C A
A B的集合C的个数为( )
B的集合C的个数为( )
A.0 B.1 C.2 D.4
21.(本小题满分14分)
已知椭圆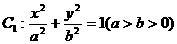 的一条准线方程是
的一条准线方程是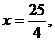 其左、右顶点分别是A、B;双曲线
其左、右顶点分别是A、B;双曲线 的一条渐近线方程为3x-5y=0.
的一条渐近线方程为3x-5y=0.
(Ⅰ)求椭圆C1的方程及双曲线C2的离心率;
(Ⅱ)在第一象限内取双曲线C2上一点P,连结AP交椭圆C1于点M,连结PB并延长交椭圆C1于点N,若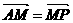 . 求证:
. 求证:

20.(本小题满分14分)
已知数列 ,设Sn是数列的前n项和,并且满足a1=1,对任意正整数n,
,设Sn是数列的前n项和,并且满足a1=1,对任意正整数n,
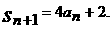
(Ⅰ)令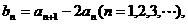 证明
证明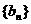 是等比数列,并求
是等比数列,并求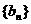 的通项公式;
的通项公式;
(Ⅱ)令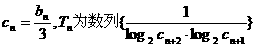 的前n项和,求
的前n项和,求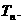
19.(本小题满分14分)
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正
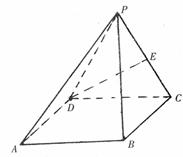 三角形,且平面PDC⊥底面ABCD,E为PC的中点。
三角形,且平面PDC⊥底面ABCD,E为PC的中点。
(I)求异面直线PA与DE所成的角;
(II)求点D到面PAB的距离.
18. (本小题满分14分)
从汽车东站驾车至汽车西站的途中要经过8个交通岗,假设某辆汽车在各交通岗遇到红灯的事件是独立的,并且概率都是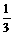 .
.
(Ⅰ)求这辆汽车首次遇到红灯前,已经过了两个交通岗的概率;
(Ⅱ)求这辆汽车在途中恰好遇到4次红灯的概率.
17.(本小题满分12分)
设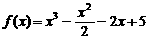 .
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)当x∈[
.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)当x∈[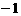 ,2]时,
,2]时, 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
16.(本小题满分12分)
已知向量 =(m-sinx,-1),
=(m-sinx,-1),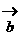 =(1,cosx),且
=(1,cosx),且
 =1,m、x∈R.
=1,m、x∈R.
(Ⅰ)把m表示为x的函数f(x),并求该函数的最小值;
(Ⅱ)把函数的图象按向量 =(
=(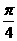 ,1)平移得到
,1)平移得到 ,求
,求 的函数式.
的函数式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com