
题目列表(包括答案和解析)
(17)(本小题满分12分)
解关于x的不等式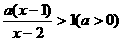 .
.
(18)(本小题满分12分)
ABCD是四边形,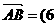 ,
,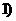 ,
,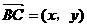 ,
,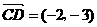 .
.
(Ⅰ)若 ∥
∥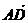 ,求x、y间的关系;
,求x、y间的关系;
(Ⅱ)若 ∥
∥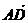 ,
,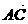 ⊥
⊥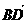 ,求x、y的值.
,求x、y的值.
(19)(本小题满分12分)
如图综9,四面体ABCD中,AB、BC、BD两两垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成角的正弦为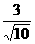 .
.
(Ⅰ)求二面角D-AC-B的平面角的正切值;
(Ⅱ)求点B到平面ACD的距离.
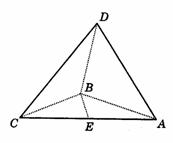
综9
(20)(本小题满分12分)
南方某林场有荒山3250亩,从1996年1月开始在该荒山上植树造林,且每年种树全部成活.第一年植树100亩,此后每年都比上一年多植树50亩.
(Ⅰ)问至少需多少年才能把此荒山全部绿化?
(Ⅱ)如果新种树苗每亩木材量为2立方米,树木每年的自然增材率为10%,那么到此荒山全部绿化后的那一年底,这林场树木的木材量总共有多少立方米?(可用1.111≈2.7)
(21)(本小题满分12分)
(Ⅰ)a取什么值时,直线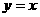 是曲线
是曲线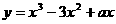 的切线?
的切线?
(Ⅱ)a取什么范围内值时,函数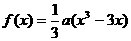 在区间(-1,1)内是减函数?
在区间(-1,1)内是减函数?
(22)(本小题满分14分)
已知抛物线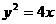 的准线与x轴交于M点,过点M作直线与这个抛物线交于两个不同的点A、B,线段AB的垂直平分线与x轴交于E(x0,0).
的准线与x轴交于M点,过点M作直线与这个抛物线交于两个不同的点A、B,线段AB的垂直平分线与x轴交于E(x0,0).
(Ⅰ)求x0的取值范围.
(Ⅱ)△ 能否是等边三角形?若能,求x0的的值;若不能,说明理由.
能否是等边三角形?若能,求x0的的值;若不能,说明理由.
(13)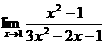 的值为________.
的值为________.
(14)正方形ABCD、ABEF有公共边AB,它们所成二面角为60°,那么异面直线AC、BF所成角的余弦值为________.
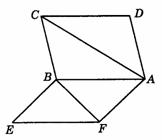
综8
(15)双曲线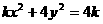 的离心率小于2,那么实数k的取值范围是________.
的离心率小于2,那么实数k的取值范围是________.
(16)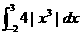 =________.
=________.
(1)sin15°cos165°的值是( ).
A.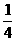 B.
B.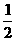 C.
C.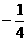 D.
D.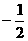
(2)已知三条直线m、n、l,三个平面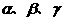 ,下面四个命题中,正确的是( ).
,下面四个命题中,正确的是( ).
A.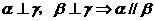 B.
B.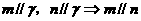
C.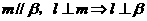 D.
D.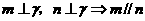
(3)已知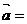 (-2,5),
(-2,5),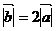 ,且
,且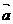 与
与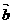 方向相反,那么
方向相反,那么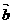 =( ).
=( ).
A.(4,-10) B.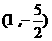 C.(-4,10) D.
C.(-4,10) D.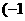 ,
,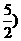
(4)函数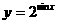 的单调递增区间是( ).
的单调递增区间是( ).
A.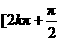 ,
,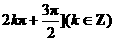 B.
B.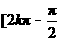 ,
,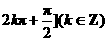
C.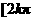 ,
,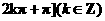 D.
D.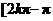 ,
,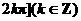
(5)一直线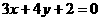 与圆
与圆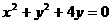 交于A、B两点,则线段AB的垂直平分线的方程是( ).
交于A、B两点,则线段AB的垂直平分线的方程是( ).
A.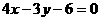 B.
B.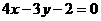
C.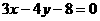 D.
D.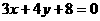
(6)已知在一个球的球心两侧有相距为7的两个平行截面,截面面积分别为9p 和16 p .那么这个球的表面积为( ).
A.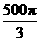 B.100 p C.64 p
D.36 p
B.100 p C.64 p
D.36 p
(7)口袋里有5个黑球和3个白球,每次任意取出一个球,若取出黑球,则放回袋中重新取球;若取出白球,则停止取球,那么正好在第4次取球后停止取球的概率是( ).
A.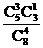 B.
B.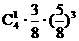
C.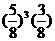 D.
D.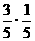
(8)若一个等差数列前3项和为34,最后3项的和为146,且所有项的和为390,则这个数列共有( ).
A.13项 B.12项 C.11项 D.10项
(9)已知函数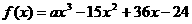 在
在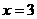 处有极值,则
处有极值,则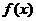 的递减区间是( ).
的递减区间是( ).
A.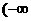 ,
, ,
,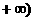 B.(1,5)
B.(1,5)
C.(2,3)
D.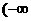 ,
, ,
,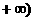
(10)F1、F2是椭圆的左、右两焦点,以F2为圆心,OF2为半径的圆与椭圆交于点M,O是原点,如果F1M正好是这个圆的一条切线,则这个椭圆的离心率是( ).
A.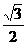 B.
B.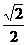 C.
C.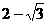 D.
D.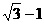
(11)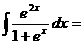 ( ).
( ).
A.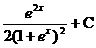 B.
B.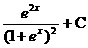
C.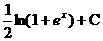 D.
D.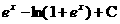
(12)已知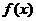 是定义在R上的奇函数,
是定义在R上的奇函数,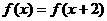 ,若当
,若当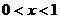 时,
时,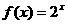 ,则
,则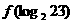 的值为( ).
的值为( ).
A.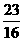 B.
B.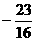 C.
C.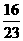 D.
D.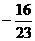
22.(I)当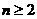 时,
时,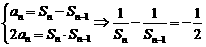 (
(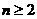 ),故
),故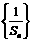 是公差为
是公差为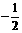 的等差数列;(Ⅱ)
的等差数列;(Ⅱ)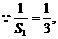 得
得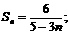 当
当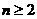 时,
时,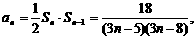 而a1=3;
而a1=3;
(Ⅲ)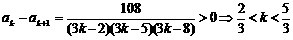 或
或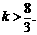 ∴当k≥3时,恒有
∴当k≥3时,恒有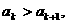 故最小k=3.
故最小k=3.
21.设分n次等量进货,∴总费用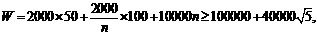
当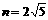 时等号成立;而f(4)=f(5)=9;故分4次或5次(最好4次)进货才能使总费用最小,
时等号成立;而f(4)=f(5)=9;故分4次或5次(最好4次)进货才能使总费用最小,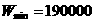 元.
元.
20.设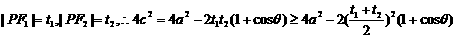
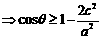 ,等号成立时
,等号成立时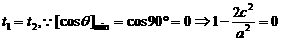
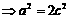 ,
,
∴椭圆C方程为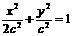 ①,而
①,而 方程为
方程为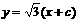 ②,联立①、②得
②,联立①、②得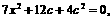
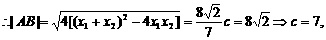 故椭圆方程为
故椭圆方程为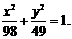
19.(I)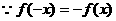 为奇函数;
为奇函数;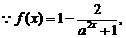 任取
任取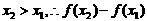
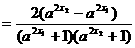 ,①当
,①当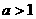 时f(x)为增函数;②当
时f(x)为增函数;②当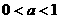 时f(x)为减函数;
时f(x)为减函数;
(Ⅱ)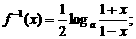 (Ⅲ)①当a>1时
(Ⅲ)①当a>1时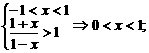 ②当0<a<1时,
②当0<a<1时,
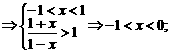
18.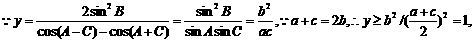
等号成立时a=c,∴2a=2b得a=b=c,故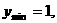 此时△ABC为正三角形.
此时△ABC为正三角形.
22. 已知数列{an}的首项a1=3,通项an与前n项和Sn之间满足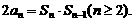
(Ⅰ)求证: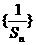 是等差数列,并求公差;
是等差数列,并求公差;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)数列{an}中是否存在正整数k,使得不等式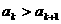 对任意不小于k的正整数都成立?若存在,求出最小的k值;若不存在,请说明理由.
对任意不小于k的正整数都成立?若存在,求出最小的k值;若不存在,请说明理由.
高三数学综合练习一答案
21.某大型商厦的家电部计划2002年销售“海豹”牌冰箱2000台,经铁路分若干次等量进货,运输费用按每台50元计算,但每次进货必须另加1万元火车车箱调度费用。冰箱进货后需租用商厦仓库存放,但仓库租用面积必须年前(2001年底)作出计划,租用面积确定以后必须租用一年(中途不能更改租用面积),仓库年租金按所租用面积能存放冰箱的最大数量乘以100元计算.问几次等量进货,才能使运输费用与仓库租金总和最小,最小总费用是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com