
题目列表(包括答案和解析)
4. 已知一个简单多面体的每一个面都是三角形,以每一个顶点为一端都有5条棱,则此多面体的棱数为 A.30 B.32 C.20 D.18
3. 下列各组向量中,共线的是 A.=(-2,3),=(4,6) B.=(2,3),=(3,2) C.=(1,-2),=(7,14) D.=(-3,2),=(6,-4)
2. 设P、Q是两个非空集合,定义P*Q={(a,b)|a∈P,b∈Q},若P={0,1,2},Q={1,2,3,4},则P*Q中元素的个数是 A.4个 B.7个 C.12个 D.16个
1. 已知双曲线的离心率为,则它的两条渐近线的夹角为 A.30º B.45º C.60º D.90º
(17)(本小题满分10分)
已知 ,
, ,
, },求
},求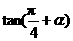 的值.
的值.
(18)(本小题满分10分)
已知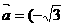 ,
, ),
), ,
, ),求
),求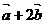 与
与 的夹角
的夹角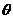 的值.
的值.
(19)(本小题满分12分)
已知等比数列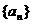 中,
中,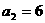 ,
,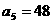 ,求
,求 及前6项和
及前6项和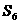 .
.
(20)(本小题满分14分)
如图综7,三棱柱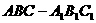 中,
中,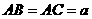 ,
,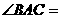 90°,顶点
90°,顶点 在底面ABC上的射影为BC边的中点M.
在底面ABC上的射影为BC边的中点M.
(Ⅰ)求证:BC垂直于过三点A1、A、M的平面;
(Ⅱ)如果平面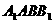 与平面ABC所成的二面角为60°,求三棱柱
与平面ABC所成的二面角为60°,求三棱柱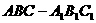 的体积.
的体积.
(21)(本小题满分14分)
设函数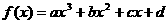 的图象与y轴的交点为P,且曲线在P点处的切线方程为
的图象与y轴的交点为P,且曲线在P点处的切线方程为 .若函数
.若函数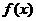 在x=2处取得极小值-16.
在x=2处取得极小值-16.
(Ⅰ)求函数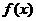 的解析式;
的解析式;
(Ⅱ)确定函数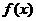 的单调减小区间.
的单调减小区间.
(22)(本小题满分14分)
已知双曲线 的离心率
的离心率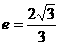 ,过点A(0,-b)和B(a,0)的直线与原点间的距离为
,过点A(0,-b)和B(a,0)的直线与原点间的距离为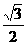 .
.
(Ⅰ)确定这个双曲线的方程;
(Ⅱ)直线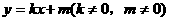 与双曲线交于两个不同的点C、D,并且C、D两点都在以A为圆心的同一个圆上,求实数m的取值范围.
与双曲线交于两个不同的点C、D,并且C、D两点都在以A为圆心的同一个圆上,求实数m的取值范围.
(13)直线 与两坐标轴所构成的三角形的面积为
与两坐标轴所构成的三角形的面积为 ,则
,则 =________.
=________.
(14) =________.
=________.
(15)如果复数 ,那么z的三角形式是________.
,那么z的三角形式是________.
(16)正方体的对角线长为l,那么它的体积为________.
(1)已知全集U=R,集合 ,
,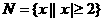 ,则(
,则(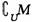 )∪(
)∪( )=( ).
)=( ).
A. B.
B.
C.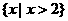 D.
D.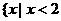 或
或
(2)函数 是( ).O
是( ).O
A.周期为π的偶函数 B.周期为π的奇函数
C.周期为1的偶函数 D.周期为1的奇函数
(3)已知空间四边形的四边长都相等,那么顺次连结各边中点的四边形一定是( ).
A.梯形 B.菱形 C.矩形 D.正方形
(4)函数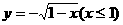 的反函数是( ).
的反函数是( ).
A. B.
B.
C.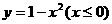 D.
D.
(5)抛物线 的准线方程是( ).
的准线方程是( ).
A.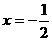 B.
B.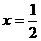 C.
C. D.
D.
(6)已知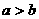 ,
, ,则下列不等式中一定成立的是( ).
,则下列不等式中一定成立的是( ).
A.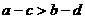 B.
B.
C.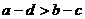 D.
D.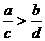
(7)若向量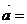 (1,1),
(1,1), (1,-1),
(1,-1), (-1,2),则
(-1,2),则 ( ).
( ).
A. B.
B.
C. D.
D.
(8) 的展开式中,常数项是( ).
的展开式中,常数项是( ).
A.第4项 B.第5项 C.第6项 D.第7项
(9)从数字1,2,3,4,5中任取两个不同的数字构成一个两位数,则这个两位数大于40的概率是( ).
A. B.
B.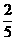 C.
C. D.
D.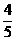
(10)曲线 在点
在点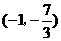 处的切线的倾斜角是( ).
处的切线的倾斜角是( ).
A.45° B.135° C.30° D.150°
(11)等差数列 中,若
中,若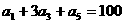 ,则
,则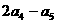 =( ).
=( ).
A.-8 B.20 C.22 D.24
(12)在正三棱锥 中,M、N分别是侧棱PB、PC的中点,若截面
中,M、N分别是侧棱PB、PC的中点,若截面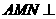 侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是( ).
侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是( ).
A.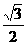 B.
B.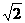 C.
C.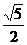 D.
D.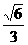
(17)(本小题满分12分)
制造某种零件,甲机床的废品率为0.04,乙机床的废品率为0.05,从这二机床生产的产品中各抽出一件作检验,求
(Ⅰ)其中恰有一件废品的概率;
(Ⅱ)其中至多有一件废品的概率;
(Ⅲ)其中没有废品的概率.
(18)(本小题满分12分)
数列 的前n项的和为
的前n项的和为 ,且
,且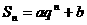 .其中
.其中 ,
,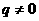 ,
, .
.
(Ⅰ)若数列 是公比为q的等比数列,求证
是公比为q的等比数列,求证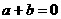 ;
;
(Ⅱ)若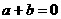 ,求证数列
,求证数列 是等比数列.
是等比数列.
(19)(本小题满分12分)
正方体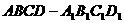 中,E、F分别为AB、BB1的中点(如图综10).
中,E、F分别为AB、BB1的中点(如图综10).
(Ⅰ)证明EF∥平面 ;
;
(Ⅱ)求二面角 的平面角的正切值;
的平面角的正切值;
(Ⅲ)若 ,求三棱锥
,求三棱锥 的体积.
的体积.

综10
(20)(本小题满分12分)
已知函数 .
.
(Ⅰ)求此函数的定义域及单调递增区间;
(Ⅱ)求此函数的极大值和极小值.
(21)(本小题满分12分)
已知甲、乙、丙三种食品的维生素A、B的含量及成本如下表:
|
|
甲 |
乙 |
丙 |
|
维生素A含量(单位/千克) |
600 |
700 |
400 |
|
维生素B含量(单位/千克) |
800 |
400 |
500 |
|
成本(元/千克) |
11 |
9 |
4 |
某食品研究所想用x千克甲种食品、y千克乙种食品、z千克丙种食品配制成100千克的混合食品,并使混合食品中至少含有56000单位的维生素A、63000单位的维生素B.
(Ⅰ)用x、y表示这种混合食品的总成本C(元);
(Ⅱ)确定x、y、z的值,使混合食品的总成本最低.
(22)(本小题满分14分)
已知双曲线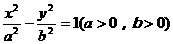 的左、右两个顶点分别为A、B,过这双曲线右焦点F2且与x轴垂直的直线交双曲线于两点P、Q、P在x轴上方,且
的左、右两个顶点分别为A、B,过这双曲线右焦点F2且与x轴垂直的直线交双曲线于两点P、Q、P在x轴上方,且 ,
,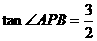 .
.
(Ⅰ)求这双曲线的方程;
(Ⅱ)若直线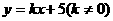 与双曲线交于不同两点M、N,且M、N都在以E(0,-1)为圆心的同一个圆上,求k的值.
与双曲线交于不同两点M、N,且M、N都在以E(0,-1)为圆心的同一个圆上,求k的值.
(13)若双曲线 的一个焦点到一条渐近线的距离为
的一个焦点到一条渐近线的距离为 ,则a=________.
,则a=________.
(14)若 ,则a=________.
,则a=________.
(15)把正方形ABCD沿对角线BD折成直二面角后,得到的三棱锥A-BCD中,有以下四个结论:
① ;
②△
;
②△ 是等边三角形;
是等边三角形;
③AB与面BCD成60°角; ④AB和CD成60°角.
那么以上结论中,正确结论的序号是________.
(16)(理科)一个袋子里有大小相同的3个红球和2个白球,从中同时取出2个,则其中含红球个数的数学期望是________.(用数字作答)
(文科)一个工厂有若干个车间,今采用分层抽样方法从全厂某天的2048件产品中抽取一个容量为128的样本进行质量检查.若一车间这一天生产256件产品,则从该车间抽取的产品件数为________.
(1)a=3是直线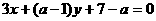 和
和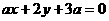 平行且不重合的( ).
平行且不重合的( ).
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分条件也非必要条件
(2)在等差数列 中,
中,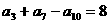 ,
, ,那么其前13项的和
,那么其前13项的和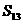 等于( ).
等于( ).
A.168 B.156 C.78 D.152
(3)已知定点M和定直线l,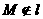 ,那么经过点M且与直线l相切的动圆的圆心的轨迹是( ).
,那么经过点M且与直线l相切的动圆的圆心的轨迹是( ).
A.直线 B.二条平行直线
C.圆 D.抛物线
(4)已知函数: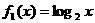 ,
,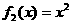 ,
,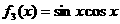 ,
,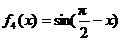 .从中任取两个相乘得到若干个函数,所得这些函数中偶函数共有( ).
.从中任取两个相乘得到若干个函数,所得这些函数中偶函数共有( ).
A.1个 B.2个 C.3个 D.4个
(5)已知向量 、
、 的夹角为90°,且
的夹角为90°,且 ,记
,记 ,
, ,若
,若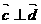 ,则k=( ).
,则k=( ).
A.-6 B.6 C.3 D.-3
(6)若点P在直线 上移动,PA、PB是圆
上移动,PA、PB是圆 的两条切线,A、B是切点,O是原点,则四边形PAOB的面积最小值为( ).
的两条切线,A、B是切点,O是原点,则四边形PAOB的面积最小值为( ).
A.24 B.16 C.8 D.4
(7)点P在曲线 上移动时,过点P曲线的切线的倾斜角的取值范围是( ).
上移动时,过点P曲线的切线的倾斜角的取值范围是( ).
A. ,
, ]
B.[
]
B.[ ,p ]
,p ]
C. ,
,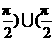 ,
, D.
D. ,
, ,p )
,p )
(8)从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者都不能从事翻译工作,则选派方案共有( ).
A.280种 B.240种 C.180种 D.96种
(9)已知圆锥轴截面是边长为2的等边三角形,当它的内接圆柱的侧面积最大时,内接圆柱的高为( ).
A.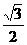 B.
B.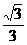 C.
C. D.
D.
(10)已知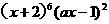 的展开式中,
的展开式中, 项的系数为100,那么实数a的值为( ).
项的系数为100,那么实数a的值为( ).
A.0或 B.
B. 或
或 C.0或
C.0或 D.
D. ,-
,-
(11)设 是由正数组成的等差数列,
是由正数组成的等差数列, 是由正数组成的等比数列,且
是由正数组成的等比数列,且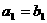 .若存在自然数m,使得
.若存在自然数m,使得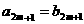 ,则必有( ).
A.
,则必有( ).
A. B.
B.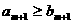
C. D.
D.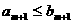
(12)二次函数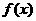 的二次项系数为正数,且对任意
的二次项系数为正数,且对任意 R都有
R都有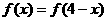 成立,若
成立,若 ,则x的取值范围是( ).
,则x的取值范围是( ).
A. B.
B. 或
或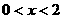
C.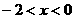 D.
D. 或
或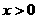
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com