
题目列表(包括答案和解析)
2.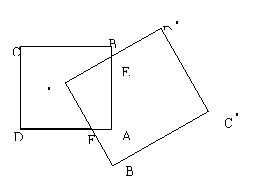 如图所示,正方形ABCD的中心是A
如图所示,正方形ABCD的中心是A ,A
,A B
B C
C D
D 也是正方形,若正方形ABCD的面积是1,且A
也是正方形,若正方形ABCD的面积是1,且A B
B >
>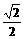 AB,AE>BE,两正方形的公共部分四边形AEA
AB,AE>BE,两正方形的公共部分四边形AEA F的面积为S,则
F的面积为S,则
A.S=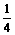 B.S>
B.S>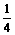
C.S<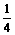 D.S的大小由正方形A
D.S的大小由正方形A B
B C
C D
D 的大小与AE的大小而定
的大小与AE的大小而定
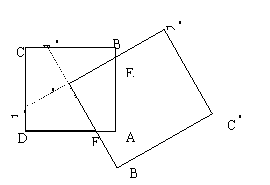 A 如图,延长D
A 如图,延长D A
A 交CD于E
交CD于E ,延长B
,延长B A
A 交BC于F
交BC于F ,则根据对称性,正方形被分成四个全等的四边形。
,则根据对称性,正方形被分成四个全等的四边形。
1.一水池有2个进水口,1 个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)
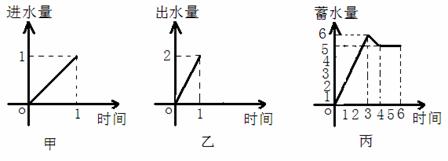
给出以下3个论断:
①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则一定能确定正确的论断是
A.① B.①② C.①③ D.①②③
4. A有一只放有x个红球,y个白球,z个黄球的箱子(x、y、z≥0,
且 ),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自
),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自
己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
(1)用x、y、z表示B胜的概率;
(2)当A如何调整箱子中球时,才能使自己获胜的概率最大?
解:(1)显然A胜与B胜为对立事件,A胜分为三个基本事件:
①A1:“A、B均取红球”;②A2:“A、B均取白球”;③A3:“A、B均取黄球”.
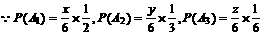
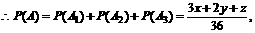
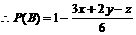
(2)由(1)知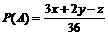 ,
,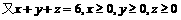
于是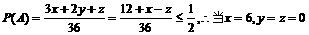 ,即A在箱中只放6个红球时,获胜概率最大,其值为
,即A在箱中只放6个红球时,获胜概率最大,其值为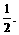
3.
把正奇数数列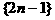 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
- - - -
- - - - -
设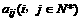 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第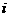 行、从左往右数第
行、从左往右数第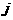 个数。
个数。
(I)若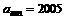 ,求
,求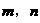 的值;
的值;
(II)已知函数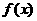 的反函数为
的反函数为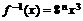
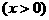 ,若记三角形数表中从上往下数第n行各数的和为
,若记三角形数表中从上往下数第n行各数的和为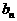 ,求数列
,求数列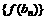 的前n项和
的前n项和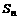 。
。
解:(I) 三角形数表中前
三角形数表中前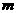 行共有
行共有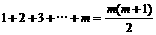 个数,
个数,
 第
第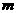 行最后一个数应当是所给奇数列中的第
行最后一个数应当是所给奇数列中的第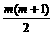 项。
项。
故第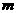 行最后一个数是
行最后一个数是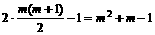
因此,使得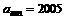 的m是不等式
的m是不等式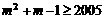 的最小正整数解。
的最小正整数解。
由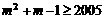 得
得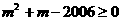

于是,第45行第一个数是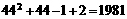
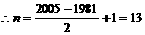
(II)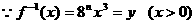 ,
, 。
。
故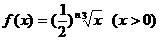
 第n行最后一个数是
第n行最后一个数是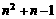 ,且有n个数,若将
,且有n个数,若将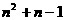 看成第n行第一个数,则第n行各数成公差为-2的等差数列,故
看成第n行第一个数,则第n行各数成公差为-2的等差数列,故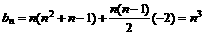 。
。
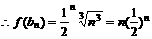
故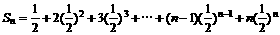
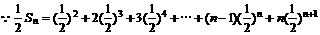 ,
,
两式相减得:
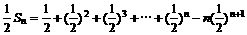
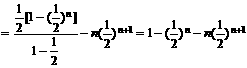

2.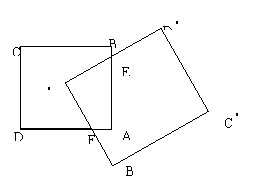 如图所示,正方形ABCD的中心是A
如图所示,正方形ABCD的中心是A ,A
,A B
B C
C D
D 也是正方形,若正方形ABCD的面积是1,且A
也是正方形,若正方形ABCD的面积是1,且A B
B >
>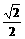 AB,AE>BE,两正方形的公共部分四边形AEA
AB,AE>BE,两正方形的公共部分四边形AEA F的面积为S,则
F的面积为S,则
A.S=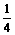 B.S>
B.S>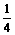
C.S<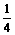 D.S的大小由正方形A
D.S的大小由正方形A B
B C
C D
D 的大小与AE的大小而定
的大小与AE的大小而定
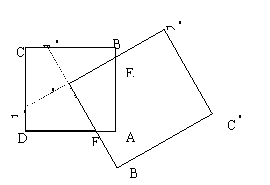 A 如图,延长D
A 如图,延长D A
A 交CD于E
交CD于E ,延长B
,延长B A
A 交BC于F
交BC于F ,则根据对称性,正方形被分成四个全等的四边形。
,则根据对称性,正方形被分成四个全等的四边形。
1.一水池有2个进水口,1 个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)
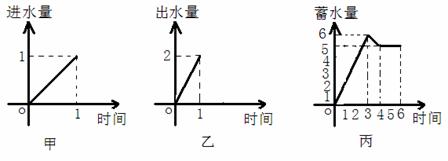
给出以下3个论断:
①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则一定能确定正确的论断是
A.① B.①② C.①③ D.①②③
4.(石中)已知曲线C: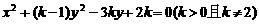 . 给出下列命题:
. 给出下列命题:
①0<k<1时,曲线C是焦点在x轴上的双曲线;
②k =1 时,曲线C是抛物线;
③1<k<2时,曲线C是焦点在y轴上的椭圆;
④k >2时,曲线C是焦点在x轴上的椭圆。其中正确命题的序号是_______(注:把你认为正确的命题的序号都填上)。答案:(2)(3)
3.(石中)平面直角坐标系中,O为坐标原点,已知A(3,1),B(-1,3),若点C满足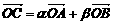 ,其中
,其中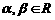 ,且
,且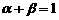 ,则点C的轨迹方程为_______.
答案:(x+2y-5=0)
,则点C的轨迹方程为_______.
答案:(x+2y-5=0)
2. (石中)设平面向量 =(2,-1),
=(2,-1), =(2,4),若存在实数m和
=(2,4),若存在实数m和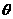 ,使向量
,使向量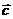 =
= +(2sin
+(2sin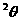 -3)
-3) ,
,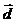 =-m
=-m +
+ sin
sin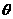 且
且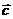 ⊥
⊥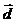 .
.
(1)求函数m=f(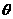 )的关系式.
)的关系式.
(2)求m的最大值和最小值
解:(1)∵ =(2,-1),
=(2,-1), =(2,4),
=(2,4),
 ﹒
﹒ =2×2+(-1)×4=0,
|
=2×2+(-1)×4=0,
| |
|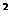 =2
=2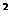 +(-1)
+(-1)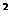 =5, |
=5, | |
|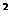 =2
=2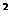 +4
+4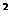 =20
=20
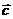 ﹒
﹒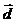 =(
=( +(2sin
+(2sin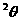 -3)
-3) )﹒(-m
)﹒(-m +
+ sin
sin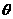 )
)
=-ma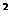 +(2sin
+(2sin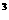
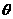 -3sin
-3sin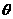 )
)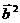 =-5m+20(2sin
=-5m+20(2sin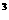
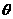 -3sin
-3sin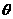 )
)
又∵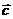 ⊥
⊥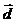 ,∴
,∴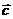 ﹒
﹒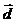 =0,即-5m+20(2sin
=0,即-5m+20(2sin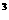
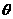 -3sin
-3sin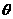 )=0
)=0
∵m=4(2sin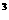
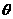 -3sin
-3sin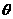 ),即f(
),即f(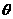 )=4(2sin
)=4(2sin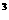
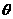 -3sin
-3sin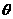 ).
).
(2)设sin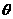 =t,则m=4(2t
=t,则m=4(2t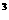 -3t),(t
-3t),(t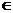 ﹝-1,1﹞),
﹝-1,1﹞),
令g(t)= 2t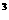 -3t (t
-3t (t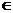 ﹝-1,1﹞), 则
﹝-1,1﹞), 则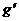 (t)=6t
(t)=6t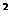 -3,
-3,
令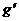 (t)=0,可得t=
(t)=0,可得t=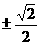 ,当t变化时,g(t) ,
,当t变化时,g(t) ,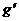 (t)的变化情况如下表:
(t)的变化情况如下表:
|
t |
﹝-1,-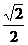 ﹚ ﹚ |
-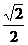 |
(-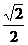 , ,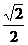 ) ) |
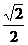 |
(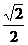 ,1﹞ ,1﹞ |
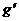 (t) (t) |
+ |
0 |
- |
0 |
+ |
|
g(t) |
↗ |
极大值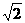 |
↘ |
极小值-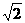 |
↗ |
又g(1)=-1,g(-1)=1,故g(t)的最大值为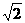 ,最小值为-
,最小值为-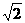 ,
,
∵m的最大值为4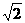 ,最小值为-4
,最小值为-4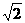 。
。
1.
高三数学题目3(石中)已知数列{a }、{b
}、{b }满足a
}满足a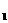 =2t(t为常数且t≠0)
,且a
=2t(t为常数且t≠0)
,且a =2t-
=2t-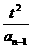 , b
, b =
=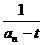 (1)判断数列{b
(1)判断数列{b }是否为等差数列,并证明你的结论。
}是否为等差数列,并证明你的结论。
(2)若b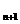 = b
= b +
+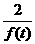 ,作数列{d
,作数列{d },使d
},使d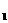 =2,d
=2,d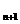 =f(d
=f(d )(n
)(n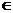 N
N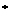 ),
),
求和A =C
=C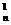 d
d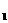 +C
+C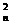 d
d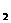 +…+C
+…+C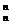 d
d 。
。
解:(1)b =
=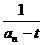 =
=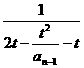 =
=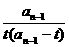 =
=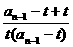 =
=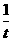 -
-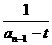 =
=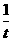 +b
+b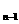 ,
,
∴b - b
- b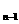 =
=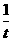 , ∴{b
, ∴{b }是等比数列。
}是等比数列。
(2)b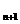 -b
-b =
=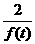 =
=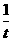 ,∴f(t)=2t,
∴d
,∴f(t)=2t,
∴d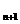 =f(d
=f(d )=2d
)=2d ,又d
,又d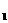 =2
=2
∴{d }是首项为2,公比为2的等比数列,即d
}是首项为2,公比为2的等比数列,即d =2
=2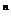
即A =2C
=2C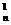 +2
+2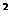 C
C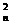 +…+2
+…+2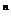 C
C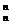 =C
=C +2C
+2C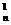 +2
+2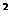 C
C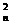 +…+2
+…+2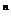 C
C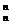 -1=3
-1=3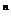 -1.
-1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com