
题目列表(包括答案和解析)
8、当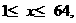 则函数
则函数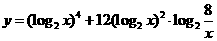 的最大值是( )
的最大值是( )
(A)9 (B)81 (C)64 (D)6
7.设双曲线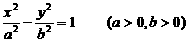 中,离心率
中,离心率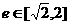 ,则两条渐近线的夹角
,则两条渐近线的夹角
θ的取值范围是 ( )
A. B.
B.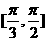 C.
C.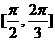 D.
D.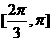
6.设数列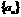 是公比为a(a≠1)首项为b的等比数列,Sn是前n项和,对任意的n∈N,点(
是公比为a(a≠1)首项为b的等比数列,Sn是前n项和,对任意的n∈N,点(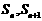 ) ( )
) ( )
A.在直线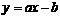 上 B.在直线
上 B.在直线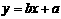 上
上
C.在直线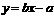 上 D.在直线
上 D.在直线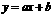 上
上
5.已知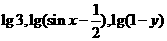 顺次成等差数列,则(
)
顺次成等差数列,则(
)
(A)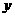 有最大值,无最小值
(B)
有最大值,无最小值
(B)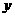 有最小值
有最小值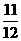 ,无最大值
,无最大值
(C)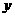 有最小值
有最小值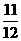 ,最大值1 (D)
,最大值1 (D)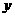 有最小值 -1,最大值1
有最小值 -1,最大值1
4.一张报纸,其厚度为a,面积为b,现将此报纸对折(既沿对边中点的连线折叠)7次,
这时报纸的厚度和面积分别是 ( )
A.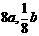 B.
B.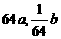 C.
C.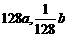 D.
D.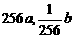
3.等比数列{an}中,设a9=-2, 则此数列的前17项之积为( )。
(A)216 (B)-216 (C)217 (D)-217
2.数列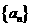 中,
中,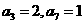 ,又数列
,又数列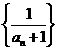 是等差数列,则
是等差数列,则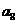 =( )
=( )
(A)0
(B)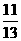 (C)
(C)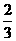 (D)-1
(D)-1
1.在数列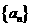 中,
中,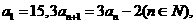 则该数列中相邻两项乘积是负数的项是( )
则该数列中相邻两项乘积是负数的项是( )
(A)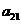 和
和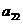 (B)
(B)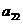 和
和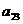 (C)
(C)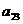 和
和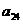 (D)
(D)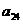 和
和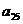
4. A有一只放有x个红球,y个白球,z个黄球的箱子(x、y、z≥0,
且 ),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自
),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自
己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
(1)用x、y、z表示B胜的概率;
(2)当A如何调整箱子中球时,才能使自己获胜的概率最大?
解:(1)显然A胜与B胜为对立事件,A胜分为三个基本事件:
①A1:“A、B均取红球”;②A2:“A、B均取白球”;③A3:“A、B均取黄球”.


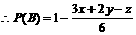
(2)由(1)知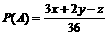 ,
,
于是 ,即A在箱中只放6个红球时,获胜概率最大,其值为
,即A在箱中只放6个红球时,获胜概率最大,其值为
3.
把正奇数数列 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
- - - -
- - - - -
设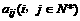 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数。
个数。
(I)若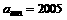 ,求
,求 的值;
的值;
(II)已知函数 的反函数为
的反函数为
 ,若记三角形数表中从上往下数第n行各数的和为
,若记三角形数表中从上往下数第n行各数的和为 ,求数列
,求数列 的前n项和
的前n项和 。
。
解:(I) 三角形数表中前
三角形数表中前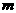 行共有
行共有 个数,
个数,
 第
第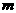 行最后一个数应当是所给奇数列中的第
行最后一个数应当是所给奇数列中的第 项。
项。
故第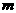 行最后一个数是
行最后一个数是
因此,使得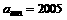 的m是不等式
的m是不等式 的最小正整数解。
的最小正整数解。
由 得
得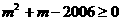

于是,第45行第一个数是

(II) ,
, 。
。
故
 第n行最后一个数是
第n行最后一个数是 ,且有n个数,若将
,且有n个数,若将 看成第n行第一个数,则第n行各数成公差为-2的等差数列,故
看成第n行第一个数,则第n行各数成公差为-2的等差数列,故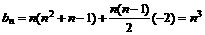 。
。

故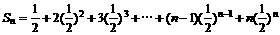
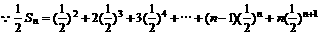 ,
,
两式相减得:
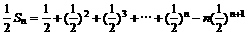

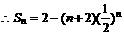
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com