
题目列表(包括答案和解析)
5.判断函数f(x)=(x-1)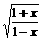 的奇偶性为____________________
的奇偶性为____________________
4.函数y=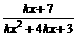 的定义域是一切实数,则实数k的取值范围是_____________
的定义域是一切实数,则实数k的取值范围是_____________
3.命题“若△ABC有一内角为 ,则△ABC的三内角成等差数列”的逆命题是( )
,则△ABC的三内角成等差数列”的逆命题是( )
A.与原命题真值相异 B.与原命题的否命题真值相异
C.与原命题的逆否命题的真值相同 D.与原命题真值相同
2.已知集合A={x| -2≤x≤7 }, B={x|m+1<x<2m-1=,若A∪B=A,则函数m的取值范围是( )A.-3≤m≤4 B.-3<m<4 C.2<m<4 D.2<m≤4
1.已知集合A={x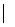 x2+(p+2)x+1=0, p∈R},若A∩R+=
x2+(p+2)x+1=0, p∈R},若A∩R+=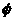 。则实数P的取值范围为
。
。则实数P的取值范围为
。
6.袋内有9个白球和3个红球,从袋内任意地顺次取出三个球(取出后不放回)。
(I)求第三次取出的球是白球的概率
 (II)当第三次取出的球是白球时,问第一次取出的球是白球的概率是多少?
(II)当第三次取出的球是白球时,问第一次取出的球是白球的概率是多少?
联想:如图,已知电路中4个开关闭合的概率都是 ,
,
且是相互独立的,求灯亮的概率。
5.若以连续掷两次骰子分别得到的点数m、n分为点P的坐标,则点P落在圆x2+y2=16内的概率为( )
A.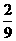 B.
B. C.
C. D.
D.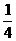
联想:(1)有红、黄、蓝三种颜色的旗帜各3面,在每种颜色的3面旗帜上分别标上号码1、2和3。现在取出3面,它们的颜色与号码均不相同的概率是 。
(2)从集合{0,1,2,3,5,7,11}中任取3个元素分别作为方程Ax+By+C=0中的A、B、C所得恰好总经过坐标原点的直线的概率是 。
(3)袋内装有大小相同的4个白球和3个黑球,从中任意摸出3个球,其中只有一个黑球的概率是 。
(4)在大小相同的6个球中,2个是红球,4个是白球,若从中任意选取3个,则所选取的3个球中至少有一个红球的概率是 。
4.已知a、b是直线,α、β、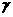 是平面。给出下列命题:
是平面。给出下列命题:
①
a∥α,a∥β,α∩β=b,则a∥b;②α⊥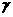 ,β⊥
,β⊥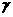 ,α∥β;
,α∥β;
③a⊥α,b⊥β,a⊥b,则α⊥β;④α∥β,β∥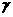 ,a⊥α,则a⊥
,a⊥α,则a⊥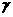 。其中正确命题的序号是( )
。其中正确命题的序号是( )
A.①②④ B.①③④ C.②④ D.②③
联想:(1)已知直线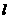 ⊥平面α,直线m
⊥平面α,直线m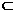 β,有下面四个命题:
β,有下面四个命题:
①α∥β ⊥m;②α⊥β
⊥m;②α⊥β ∥m;③
∥m;③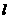 ∥m
∥m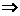 α⊥β;④
α⊥β;④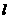 ∥m
∥m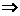 α∥β。其中正确的两个命题是( )
α∥β。其中正确的两个命题是( )
A.①与② B.③与④ C.②与④ D.①与③
(2)已知集合A、B、C,A={直线},B={平面},C=A∪B若a∈A,b∈B,c∈C,在下面命题中
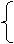
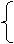
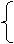
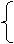 a⊥b
a⊥b
a∥b
a∥b
a⊥b
a⊥b
a∥b
a∥b
① 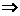 a∥c ②
a∥c ②
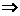 a⊥c ③
a⊥c ③ 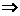 a∥c ④
a∥c ④
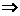 a⊥ c
a⊥ c
c⊥b c∥b b∥c c⊥b
正确命题的序号是 。(注:把你认为正确的序号都填上)
(3)若a、b是两条异面直线,则存在惟一的平面β,满足( )
A.a∥β且b∥β B.a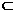 β且b∥β C.a⊥β且b⊥β D.a
β且b∥β C.a⊥β且b⊥β D.a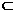 β且b⊥β
β且b⊥β
3.设函数y=(cosx-m)2-1,当cosx=-1时,取最大值,当cosx=m时,取最小值,则实数m必是( )
A.0≤m≤1 B.-1≤m≤0 C.m≤-1 D.m≥1
联想:(1)函数y=asinx+bcosx(x∈R)的最大值为 ,则a+b的最小值为( )
,则a+b的最小值为( )
A.2 B.-2
B.-2 C.
C.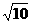 D.-
D.-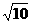
(2)若函数y=2sinx+ cosx+4的最小值为1,则a= 。
cosx+4的最小值为1,则a= 。
(3)若函数y=cos2x+asinx+1的最大值为2,则a= 。
(4)函数y=sinx+cosx+sinxcosx的最大值为 ,最小值为 。
2.已知y=f (x+1)是奇函数,且f (x)的图象关于直线x=2对称,当0≤x≤1时,f (x)=2x,则f (log224)的值为( )
A.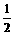 B.
B. C.
C. D.
D.
联想:(1)函数y=x3的图象在点(1,1)处的切线方程为( )
A.y=x B.y=2x-1 C.y=3x-2 D.y=4x-3
(2)函数y=lg(1-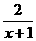 )的图象( )
)的图象( )
A.关于原点对称 B.关于x轴对称 C.关于y轴对称 D.关于直线x=1对称
(3)函数f (x)= 的奇偶性是( )
的奇偶性是( )
A.奇函数 B.偶函数 C.奇偶兼备 D.非奇非偶函数
(4)已知函数f (x)满足f (x2-3)=lg ,则y=f (x)在定义域内( )
,则y=f (x)在定义域内( )
A.是奇函数且是增函数 B.是奇函数且是减函数
C.是偶函数 D.是增函数,但既不是奇函数也不是偶函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com