
题目列表(包括答案和解析)
17.(本小题满分12分)
已知a=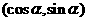 ,b=
,b=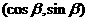 ,且
,且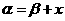 ,
,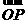 =a + b,
=a + b,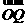 = a - b ,记
= a - b ,记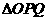 的面积为函数
的面积为函数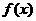 (其中
(其中 为坐标原点) .
为坐标原点) .
(1)求函数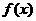 的的表达式;
的的表达式;
(2) 求函数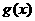 =m
=m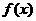 +3的最大值与最小值.
+3的最大值与最小值.
18(本小题满分12分)
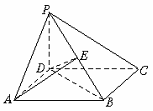
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
求证:(1)平面PAC⊥平面PBD;
(2)求PC与平面PBD所成的角;
(3)在线段PB上是否存在一点E,使得PC⊥平面ADE?若存在,请加以证明,并求此时二面角A-ED-B的大小;若不存在,请说明理由.
 19 (本小题满分12分)
19 (本小题满分12分)
设函数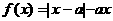 ,其中
,其中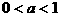 为常数。
为常数。
(I)解不等式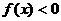 ;
;
(II)试推断函数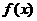 是否存在最小值,若存在,求出最小值;若不存在,说明理由。20.(本小题共12分)
是否存在最小值,若存在,求出最小值;若不存在,说明理由。20.(本小题共12分)
已知等差数列{an}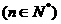 的第2项为8,前10项的和为185。
的第2项为8,前10项的和为185。
(I)求数列{an}的通项公式;
(II)若从数列{an}中依次取出第2项,第4项,第8项,…,第2n项,…,按取出顺序组成一个新数列{bn},试求数列{bn}的前n项和Sn;
(III)设Tn=n(9+an),试比较Sn与Tn的大小,并说明理由。
试推断函数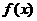 是否存在最小值,若存在,求出最小值;若不存在,说明理由。
是否存在最小值,若存在,求出最小值;若不存在,说明理由。
16.设函数f(x)=sin(wx+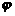 )(w>0,-
)(w>0,-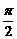 <
<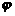 <
<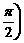 ,给出以下四个论断:
,给出以下四个论断:
①它的周期为π; ②它的图象关于直线x=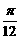 对称;
对称;
③它的图象关于点(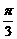 ,0)对称; ④在区间(-
,0)对称; ④在区间(-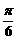 ,0)上是增函数.
,0)上是增函数.
以其中两个论断为条件,另两个论断作结论写出你认为正确的一个命题:
________________________________________________________________________.
15.设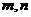 是两条不同的直线,
是两条不同的直线,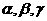 是三个不同的平面,给出下列五个命题:
是三个不同的平面,给出下列五个命题:
①若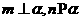 ,则
,则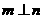 ;②若
;②若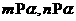 ,则
,则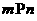 ;③若
;③若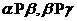 ,
,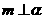 则
则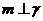 ;④若
;④若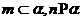 ,
,
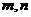 共面,则
共面,则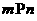 ;⑤若
;⑤若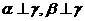 ,则
,则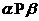 .则以上命题中,是真命题的是 .
.则以上命题中,是真命题的是 .
14.有三个球和一个正方体,第一个球与正方体各个面相内切,第二个球与正方体各条棱相切,第三个球过正方体各顶点,则这三个球的面积之比为___________.
13. 已知实数x,y满足不等式组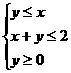 ,那么目标函数
,那么目标函数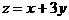 的最大值是______________。
的最大值是______________。
12.已知椭圆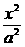 +y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|·|PF2|的值为
+y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|·|PF2|的值为
A.1 B.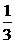 C.
C.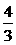 D.
D.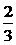
11.如图,正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则动点P的轨迹是
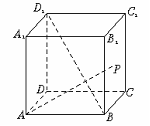
A.线段B1C
B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段
10. 已知O是△ABC所在平面上一点,若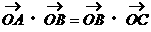 =
=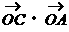 ,则O是△ABC的( )
,则O是△ABC的( )
A. 垂心 B. 重心 C. 外心 D. 内心
9. 直线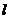 是双曲线
是双曲线 的右准线,以原点为圆心且过双曲线的焦点
的圆,被直线
的右准线,以原点为圆心且过双曲线的焦点
的圆,被直线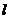 分成弧长为2∶1的两段圆弧,则该双曲线的离心率是
( )
(A)
分成弧长为2∶1的两段圆弧,则该双曲线的离心率是
( )
(A)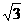 .
(B)
.
(B)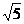 .
(C)
.
(C)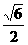 .
(D)
.
(D)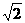 .
.
8.已知抛物线y=ax2的焦点为F,准线l与对称轴交于点R,过抛物线上一点P(1,2)作PQ⊥l,垂足为Q,则梯形PQRF的面积为
A.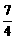 B.
B.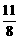 C.
C.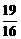 D.
D.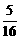
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com