
题目列表(包括答案和解析)
16、椭圆C1: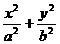 =1(a>b>0)的左右顶点分别为A、B.点P双曲线C2:
=1(a>b>0)的左右顶点分别为A、B.点P双曲线C2: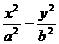 =1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.(1)求P点的坐标;(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率,若不能,请说明理由.
=1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.(1)求P点的坐标;(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率,若不能,请说明理由.
15、某集团准备兴办一所中学,投资1200万用于硬件建设.为了考虑社会效益和经济利益,对该地区教育市场进行调查,得出一组数据列表(以班为单位)如下:
|
|
班级学生数 |
配备教师数 |
硬件建设(万元) |
教师年薪(万元/人) |
|
初中 |
60 |
2.0 |
28 |
1.2 |
|
高中 |
40 |
2.5 |
58 |
1.6 |
根据有关规定,除书本费、办公费外,初中生每年可收取学费600元,高中生每年可收取学费1500元.因生源和环境等条件限制,办学规模以20至30个班为宜.根据以上情况,请你合理规划办学规模使年利润最大,最大利润多少万元?(利润=学费收入-年薪支出)
14、椭圆 的左、右焦点分别为F1、F2,右顶点为A,M为椭圆C1上任意一点,且
的左、右焦点分别为F1、F2,右顶点为A,M为椭圆C1上任意一点,且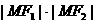 的最小值为
的最小值为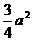 .(1)求椭圆C1的离心率;(2)设双曲线C2以椭圆C1的焦点为顶点,顶点为焦点;在第一象限内任取双曲线C2上一点P,试问是否存在常数
.(1)求椭圆C1的离心率;(2)设双曲线C2以椭圆C1的焦点为顶点,顶点为焦点;在第一象限内任取双曲线C2上一点P,试问是否存在常数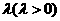 ,使得
,使得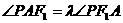 恒成立?证明你的结论.
恒成立?证明你的结论.
13、已知动点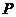 与双曲线
与双曲线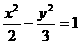 的两个焦点
的两个焦点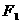 、
、 的距离之和为定值,且
的距离之和为定值,且
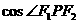 的最小值为
的最小值为 .(I)求动点
.(I)求动点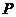 的轨迹方程; (II)若已知
的轨迹方程; (II)若已知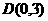 ,
,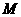 、
、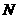 在动点
在动点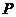 的轨迹上且
的轨迹上且 ,求实数
,求实数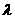 的取值范围.
的取值范围.
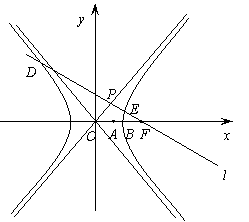
12、已知双曲线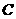 :
: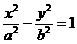
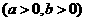 ,
, 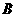 是右顶点,
是右顶点,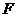 是右焦点, 点
是右焦点, 点 在
在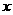 轴正半轴上,且满足
轴正半轴上,且满足 成等比数列,过
成等比数列,过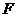 作双曲线
作双曲线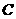 在第一、三象限的渐近线的垂线
在第一、三象限的渐近线的垂线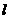 ,垂足为
,垂足为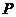 .
.
(Ⅰ)求证: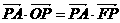 ;(Ⅱ)若
;(Ⅱ)若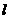 与双曲线
与双曲线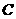 的左、右两支分别相交 于点
的左、右两支分别相交 于点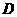 、
、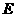 ,求双曲线
,求双曲线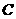 的离心率
的离心率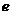 的取值范围.
的取值范围.
11、试问: 是否存在常数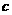 ,使得不等式
,使得不等式
对任意的正数 均成立,请证明你的结论.
均成立,请证明你的结论.
10、某种车辆,购车费10万元,每年交保险费、养路费及汽油费合计9千元,汽车的维修费平均为:第一年2千元,第二年4千元,第三年6千元,依等差数列逐年递增,问使用多少年平均费用最少?
9、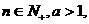 求证:
求证: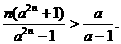
8、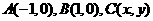 满足
满足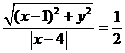 ,则
,则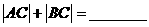
7、椭圆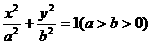 的左焦点为F,A
的左焦点为F,A 是两个顶点,如果点F到直线AB的距离等于
是两个顶点,如果点F到直线AB的距离等于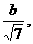 那么该椭圆的离心率等于_____
那么该椭圆的离心率等于_____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com