
题目列表(包括答案和解析)
4.若将函数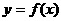 图象按向量
图象按向量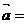 (
(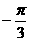 ,
,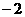 )平移后,得到函数
)平移后,得到函数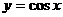 的图象,则原图象的函数解析式是:
的图象,则原图象的函数解析式是:
A.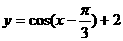 B.
B.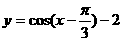
C.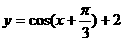 D.
D.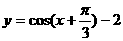
3.直线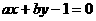 在
在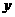 轴上的截距为1,且它的倾斜角是直线
轴上的截距为1,且它的倾斜角是直线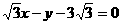 的倾斜角的2倍,则
的倾斜角的2倍,则
A.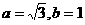 B.
B. 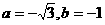 C.
C. 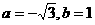 D.
D. 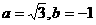
2.已知函数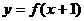 的图象过点(3,2),则函数
的图象过点(3,2),则函数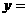
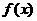 的图象关于
的图象关于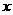 轴的对称图形一定过点
轴的对称图形一定过点
A. (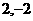 ) B.
) B.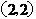 C. (
C. (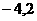 ) D. (
) D. (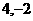 )
)
1.等比数列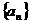 中,
中,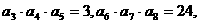 则
则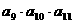 的值为
的值为
A.48 B.72 C.144 D.192
(15)(本小题满分14分)
解关于x的不等式
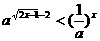 ,(a>0且a≠1)。
,(a>0且a≠1)。
(16)(本小题满分14分)
已知:定义在R上的函数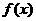 为奇函数,且在
为奇函数,且在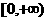 上是增函数。
上是增函数。
(Ⅰ)求证: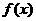 在
在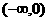 上也是增函数;
上也是增函数;
(Ⅱ)对任意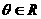 ,求实数m,使不等式
,求实数m,使不等式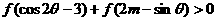 恒成立。
恒成立。
(17)(本小题满分14分)
在长方体ABCD-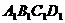 中,AB=2,
中,AB=2,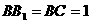 ,E为
,E为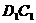 的中点,连结ED,EC,EB和DB。
的中点,连结ED,EC,EB和DB。
(Ⅰ)求证:平面EDB⊥平面EBC;
(Ⅱ)求二面角E-DB-C的正切值;
(Ⅲ)求异面直线EB和DC的距离。
(18)(本小题满分14分)
某造纸厂拟建一座平面图形为矩形且面积为200平方米的二级污水处理池(平面图如图所示),池的深度一定,池的外圈周壁建造单价为每米400元,中间一条隔壁建造单价为每米100元,池底建造单价每平方米60元(池壁厚度忽略不计)。
(Ⅰ)设污水处理池的长为x米时,写出总造价f(x)的解析式;
(Ⅱ)污水处理池的长设计为多少米时,可使总造价最低。

(19)(本小题满分14分)
已知椭圆c: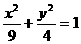 ,将椭圆c平移,中心移到点(1,2),成为椭圆c’。
,将椭圆c平移,中心移到点(1,2),成为椭圆c’。
(Ⅰ)求椭圆c’的方程;
(Ⅱ)椭圆c’上存在关于直线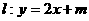 对称的不同的两点,求出m的范围。
对称的不同的两点,求出m的范围。
(20)(本小题满分14分)
已知函数 ,满足条件:
,满足条件:
①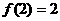 ;②
;②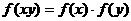 ;③
;③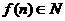 ;
;
④当x>y时,有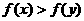 。
。
(Ⅰ)求f(1),f(3)的值;
(Ⅱ)由f(1),f(2),f(3)的值,猜想f(n)的解析式;
(Ⅲ)证明你猜想的f(n)的解析式的正确性。
(11)已知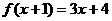 ,则
,则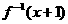 =________________。
=________________。
(12)在一个棱长为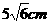 的正四面体内有一点P,它到三个面的距离分别是1cm,2cm,3cm,则它到第四个面的距离为_______________cm。
的正四面体内有一点P,它到三个面的距离分别是1cm,2cm,3cm,则它到第四个面的距离为_______________cm。
(13)设等比数列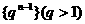 的前n项和为
的前n项和为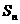 ,前n+1项的和为
,前n+1项的和为 ,则
,则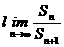 =___________________。
=___________________。
(14)抛物线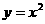 和圆
和圆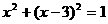 上最近两点的距离是_________________。
上最近两点的距离是_________________。
(1)设集合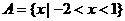
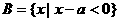 ,若
,若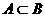 ,则a的取值范围是( )
,则a的取值范围是( )
(A)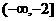 (B)
(B)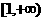 (C)
(C)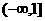 (D)
(D)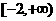
(2)已知二面角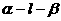 ,直线
,直线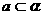 ,
,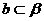 ,且a与l不垂直,b与l不垂直,那么( )
,且a与l不垂直,b与l不垂直,那么( )
(A)a与b可能垂直,但不可能平行 (B)a与b可能垂直,也可能平行
(C)a与b不可能垂直,但可能平行 (D)a与b不可能垂直,也不可能平行
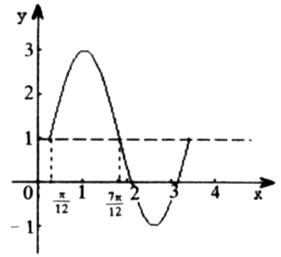
(3)函数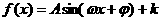 在一个周期内的图象如图所示,函数
在一个周期内的图象如图所示,函数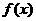 解析式为( )
解析式为( )
(A)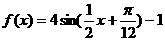
(B)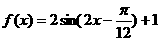
(C)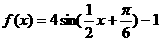
(D)
(4)若椭圆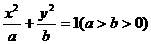 ,双曲线
,双曲线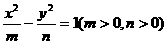 有相同的焦点
有相同的焦点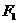 ,
,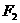 ,P是两曲线的交点,则
,P是两曲线的交点,则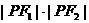 的值是( )
的值是( )
(A) (B)
(B)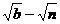 (C)a-m (D)b-n
(C)a-m (D)b-n
(5)如图,O为直二面角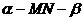 的棱MN上的一点,射线OE,OF分别在
的棱MN上的一点,射线OE,OF分别在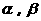 内,且∠EON=∠FON=45°,则∠EOF的大小为( )
内,且∠EON=∠FON=45°,则∠EOF的大小为( )
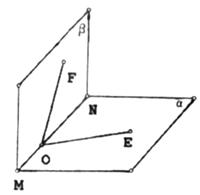
(A)30° (B)45° (C)60° (D)90°
(6)在等差数列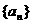 中,
中, 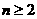 ,公差d<0,前n项和是
,公差d<0,前n项和是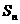 ,则有( )
,则有( )
(A)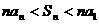 (B)
(B)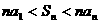
(C)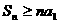 (D)
(D)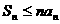
(7)8种不同的商品,选出5种放入5个不同的柜台中,如果甲、乙两种商品不能放入第5号柜台中,那么不同的放法共有( )
(A)3360种 (B)5040种 (C)5880种 (D)2160种
(8)下列四个命题:
①满足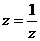 的复数只有
的复数只有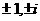 ;
;
②若a,b是两个相等的实数,则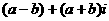 是纯虚数;
是纯虚数;
③复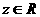 的充要条件是
的充要条件是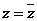 ;
;
④复平面内x轴即实轴,y轴即虚轴。
其中正确的有( )
(A)1个 (B)2个 (C)3个 (D)4个
(9)在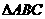 中,
中,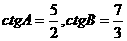 ,则角C等于( )
,则角C等于( )
(A)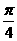 (B)
(B)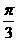
(C)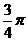 (D)
(D)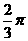
(10)过抛物线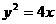 的焦点作直线与此抛物线交于P,Q两点,那么线段PQ中点的轨迹方程是( )
的焦点作直线与此抛物线交于P,Q两点,那么线段PQ中点的轨迹方程是( )
(A)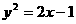 (B)
(B)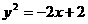
(C)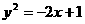 (D)
(D)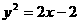
第Ⅱ卷(非选择题共100分)
20.(本小题满分12分)
已知定义域为[0,1]的函数f(x)同时满足:
(1)对于任意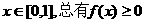 ;
;
(2)f(1)=1
(3)若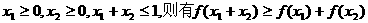
(Ⅰ)试求f(0)的值;
(Ⅱ)试求函数f(x)的最大值;
(Ⅲ)(理科学生做,文科学生不做)
试证明:满足上述条件的函数f(x)对一切实数x,都有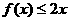 .
.
19.(本小题满分16分)
在直角坐标平面内,已知两点A(-2,0)及B(2,0),动点Q到点A的距离为6,线段BQ的垂直平分线交AQ于点P.
(Ⅰ)证明|PA|+|PB|为常数,并写出点P的轨迹T的方程;
(Ⅱ)(理科学生做)过点B的直线l与曲线T相交于M、N两点,线段MN的中点R与点S(-1,0)的连线的纵截距为t,试求t的取值范围.
 (文科学生做)过点B且倾斜角为120°的直线l与曲线T相交于M、N两点,试求△AMN的面积.
(文科学生做)过点B且倾斜角为120°的直线l与曲线T相交于M、N两点,试求△AMN的面积.
18.(本小题12分)
有一组数据: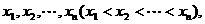 它们的算术平均值为10,若去掉其中最大的一个,余下的数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11.
它们的算术平均值为10,若去掉其中最大的一个,余下的数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11.
(Ⅰ)求出第一个数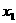 关于n的表达式及第n个数
关于n的表达式及第n个数 关于n的表达式.
关于n的表达式.
(Ⅱ)若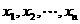 都是正整数,试求第n个数
都是正整数,试求第n个数 的最大值,并举出满足题目要求且
的最大值,并举出满足题目要求且 取到最大值的一组数据.
取到最大值的一组数据.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com