
题目列表(包括答案和解析)
3.在
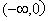 上为增函数的是
上为增函数的是
A. 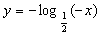 B.
B. 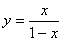
C. 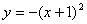 D.
D.
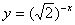
2.函数 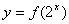 的定义域是[-1,1],则函数
的定义域是[-1,1],则函数
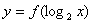 的定义域是
的定义域是
A.
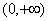 B.
B.
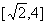 C.
C.
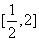 D.[1,2]
D.[1,2]
1.从集合A={-1,1}到集合A能建立不同函数的个数是
A.1个 B.2个 C.3个 D.4个
㈠结合教学内容,借助软件和技术,制作课例
随着计算机的普及,软件的技术在教学中的作用正逐步体现。对于本章的教学内容,有许多可以与计算机辅助教学相结合。计算机强大的计算功能、图形处理能力能很好地体现数列、函数的运动变化过程,对于学生理解极限概念很有帮助。
㈡结合本章内容对学生进行思想教育
通过介绍刘徽“割圆术”,对学生进行爱国主义教育,激发学生的民族自豪感,为祖国的繁荣昌盛而努力学习的热情;通过对极限内容的教学,使学生从量变中认识质变,从有限中认识无限,从近似中认识精确,帮助他们树立运动变化的辩证唯物主义观点。
4. 明确函数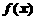 点
点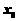 处连续的三个条件。
处连续的三个条件。
3.掌握一些极限常用技巧
1) 无穷小量分出法求分式极限(对学生不必提无穷小量概念),一般分子、分母同除以n的最高次幂再计算。
例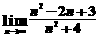
2)“零因子”消去法
例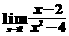
3)化无限项为有限项
例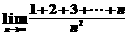
4)裂项化简
例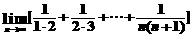
2.在极限教学中应注意:
1) 运用极限四则运算法则有前提,必须具备条件:数列{an}、{bn}极限均存在。
例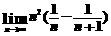
2)极限的代数和形式即“和的极限等于极限的和”只适用于有限多项相加。
例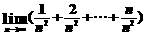
3)当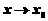 ,
,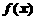 是否存在极限与
是否存在极限与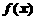 在
在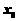 处是否有定义无关。
处是否有定义无关。
1.如何让学生从数列变化的趋势理解数列极限的概念?
6. 函数极限的应用纳入选修(Ⅱ)第三章导数。
教学中应当注意:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com