
题目列表(包括答案和解析)
基础训练9答案一、1.D 2.C 3.D
二、4.2 5.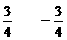 三、6.
三、6.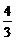 1 7.
1 7.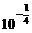 8.(1)既不是奇函数,也不是偶函数(2)a≤-
8.(1)既不是奇函数,也不是偶函数(2)a≤-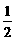 时,f(x)最小值为
时,f(x)最小值为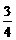 -a;-
-a;-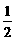 <a≤
<a≤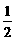 时,f(x)的最小值是a2+1;当a>
时,f(x)的最小值是a2+1;当a>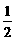 时,f(x)最小值是a+
时,f(x)最小值是a+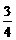 .
.
基础训练10答案
g(t)的最小值为0. 提示:讨论对称轴x=-1与区间端点t,t+1的关系. 8.[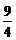 ,18]
,18]
基础训练8答案一、1.C 2.D 3.B
二、4.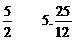
7.f(x)在(0,1],[-1,0)上为减函数;在[1,+∞),(-∞,-1)上为增函数. g(x)在(-∞,0),(0,+∞)上为增函数. 8.(1)证明略(-∞,0),(0,+∞)均为递增区间. (2)0,0,f(x2)-5f(x)g(x)=0.
基础训练7答案
(2)[-5,-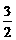 π
π ∪(-
∪(-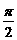 ,
,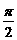 )∪(
)∪(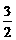 π,5
π,5 (3)令u=2x,t=log2x那么中间变量u、t的值域都相同(都为原函数的定义域),由u=2x,x∈[-1,1],∴
(3)令u=2x,t=log2x那么中间变量u、t的值域都相同(都为原函数的定义域),由u=2x,x∈[-1,1],∴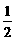 ≤2x≤2,则
≤2x≤2,则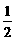 ≤log2x≤2,∴
≤log2x≤2,∴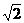 ≤x≤4,故f(log2x)的定义域为[
≤x≤4,故f(log2x)的定义域为[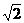 ,4]. 8.f(x)=-
,4]. 8.f(x)=-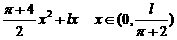
基础训练6答案
7.(1)f-1(x)=1+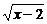 (x>2) (2)f-1(x)=
(x>2) (2)f-1(x)=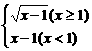 8.y=
8.y=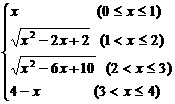
基础训练5答案
提示: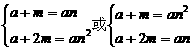 但要注意元素互异性,n≠1.
但要注意元素互异性,n≠1.
7.{x|2≤x≤3或x=1},{2},{x|x<1或x>3},{x|x≤1或x>2},U,  8.{0,1,-
8.{0,1,-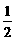 }.
}.
提示:不要忽视B= 的情形.
的情形.
基础训练4答案
8.已知函数y=log2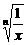 (n∈N*).
(n∈N*).
(1)当n=1,2,3,…时,已知函数的图象和直线y=1的交点的横坐标依次记为a1,a2,a3,….
求证:a1+a2+a3+…+an<1.
(2)对每一个n∈N*,设An、Bn为已知函数图象上与x轴距离为1的两点,求证:n取任意一个正整数时,以线段AnBn为直径的圆都与一条定直线相切,并求这条直线的方程和切点的坐标.
基础训练1答案
7.(2002年上海高考题)已知函数f(x)=a·bx的图象过A(4,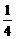 )和B(5,1)
)和B(5,1)
(1)求函数f(x)的解析式;
(2)记an=log2f(n),n是正整数,Sn是数列{an}的前n项和,解关于n的不等式anSn≤0.
(3)对于(2)中的an与Sn,96是否为数列{anSn}中的项?若是,则求出相应的项数;若不是,则说明理由.
6.在5和81之间插入两个正数,使前三个数成等差数列,后三个数成等比数列,求这两个数的和.
5.已知x、y为正实数,且x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则 的取值范围是_________.
的取值范围是_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com