
题目列表(包括答案和解析)
7. 电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首
尾必须播放公益广告,则共有 种不同的播放方式(结果用数值表示).
6. 已知函数 是定义在
是定义在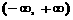 上的偶函数. 当
上的偶函数. 当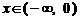 时,
时,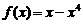 ,则
,则
当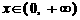 时,
时,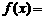 .
.
5. 已知圆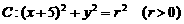 和直线
和直线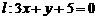 . 若圆
. 若圆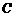 与直线
与直线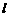 没有公共
没有公共
点,则 的取值范围是
.
的取值范围是
.
4. 不等式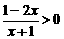 的解集是
.
的解集是
.
3. 函数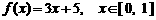 的反函数
的反函数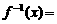 .
.
2. 方程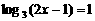 的解
的解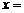 .
.
1. 计算: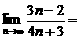 .
.
(17)本小题主要考查函数的单调性及不等式的基础知识,考查数学推理判断能力.满分12分.
解:函数 的定义域为
的定义域为
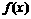 在
在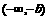 内是减函数,
内是减函数,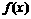 在
在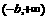 内也是减函数 ……4分
内也是减函数 ……4分
证明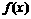 在
在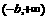 内是减函数
内是减函数
取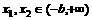 ,且
,且 ,那么
,那么
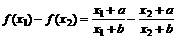
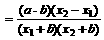 ……6分
……6分
∵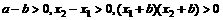
∴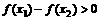
即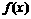 在
在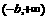 内是减函数
……9分
内是减函数
……9分
同理可证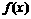 在
在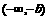 内是减函数
……12分
内是减函数
……12分
(18)本小题主要考查复数的基本概念和基本运算,考查综合运用复数的知识解决问题的能力.满分12分.
解:(Ⅰ)由 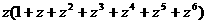
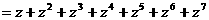
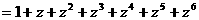 ,
,
得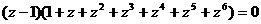 . ……4分
. ……4分
因为 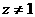 ,
,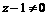 ,
,
所以 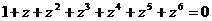 . ……6分
. ……6分
(Ⅱ)因为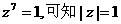 ,
,
所以 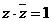 ,而
,而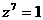 ,所以
,所以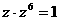 ,
,
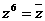 ,同理
,同理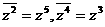 ,
,
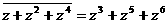 .
.
由(Ⅰ)知 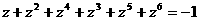 ,
,
即 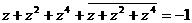 ,
,
所以
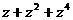 的实部为
的实部为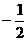 , ……8分
, ……8分
而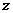 的辐角为
的辐角为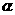 时,复数
时,复数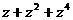 的实部为
的实部为
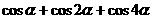 ,
,
所以 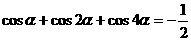 ……12分
……12分
(19)本小题主要考查线面关系的基本概念,考查运用直线与直线、直线与平面的基本性质进行计算和证明的能力.满分12分.
(Ⅰ)证明:由已知,
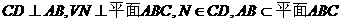 ,
,
∴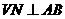 .
.
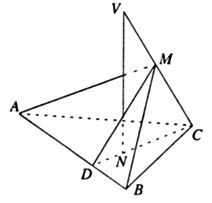
∴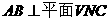 . ……2分
. ……2分
又V、M、N、D都在VNC所在平面内,
所以,DM与VN必相交,且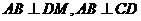 ,
,
∴∠MDC为二面角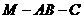 的平面角. ……4分
的平面角. ……4分
(Ⅱ)证明:由已知,∠MDC=∠CVN,
在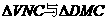 中,
中,
∠NCV=∠MCD,
又∵∠VNC=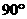 ,
,
∴∠DMC=∠VNC=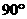 .
.
故有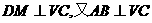 , ……6分
, ……6分
∴ . ……8分
. ……8分
(Ⅲ)解:由(Ⅰ)、(Ⅱ),
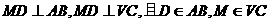 ,
,
∴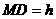 .
.
又∵∠ .
.
在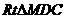 中,
中,
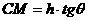 . ……10分
. ……10分
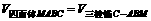
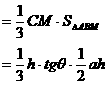
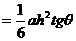 . ……12分
. ……12分
(20)本小题主要考查等差数列、等比数列的基础知识,考查观察、猜想并进行证明的数学思想方法.满分12分.
解:(I)∵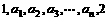 成等比数列,
成等比数列,
∴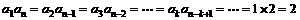 ,
,
∴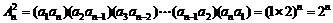
∴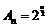 ……4分
……4分
∵ 成等差数列,∴
成等差数列,∴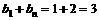 ,
,
∴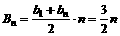
所以,数列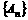 的通项
的通项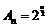 ,数列
,数列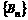 的通项
的通项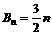 ……6分
……6分
(II)∵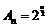 ,
,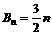 ,
,
∴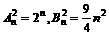 ,
,
要比较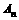 与
与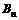 的大小,只需比较
的大小,只需比较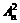 与
与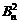 的大小,也即比较当
的大小,也即比较当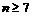 时,
时,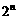 与
与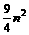 的大小.
的大小.
当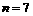 时,
时,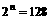 ,
,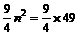 ,得知
,得知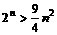 ,
,
经验证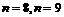 时,均有命题
时,均有命题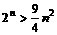 成立.
成立.
猜想当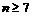 时有
时有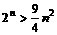 .用数学归纳法证明. ……9分
.用数学归纳法证明. ……9分
(i)当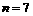 时,已验证
时,已验证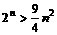 ,命题成立.
,命题成立.
(ii)假设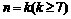 时,命题成立,即
时,命题成立,即
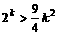 ,
,
那么 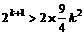
又当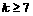 时,有
时,有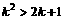
∴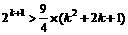
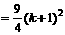
这就是说,当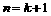 时,命题
时,命题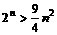 成立.
成立.
根据(i)、(ii),可知命题对于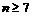 都成立.
都成立.
故当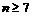 时,
时,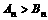 ……12分
……12分
(21)本小题主要考查建立函数关系、不等式的性质和解法等内容,考查运用数学知识解决实际问题的能力.满分12分.
解:(Ⅰ)由题意得
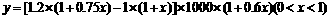 ,
,
……4分
整理得 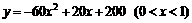 . ……6分
. ……6分
(Ⅱ)要保证本年度的利润比上年度有所增加,当且仅当
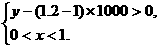
即 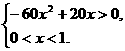 ……9分
……9分
解不等式得
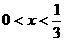 .
.
答:为保证本年度的年利润比上年度有所增加,投入成本增加的比例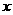 应满足
应满足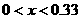 .
……12分
.
……12分
(22)本小题考查直线与抛物线的基本概念及位置关系,考查运用解析几何的方法解决数学问题的能力.满分14分.
解:(Ⅰ)直线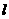 的方程为
的方程为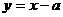 ,
,
将  ,
,
得 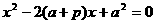 . ……2分
. ……2分
设直线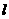 与抛物线两个不同交点的坐标为
与抛物线两个不同交点的坐标为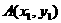 、
、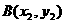 ,
,
则 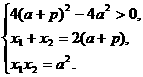 ……4分
……4分
又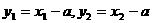 ,
,
∴ 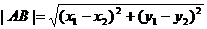
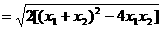
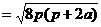 . ……6分
. ……6分
∵ 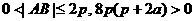 ,
,
∴ 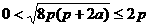 .
.
解得 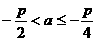 . ……8分
. ……8分
(Ⅱ)设AB的垂直平分线交AB于点Q,令坐标为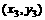 ,则由中点坐标公式,得
,则由中点坐标公式,得
 ,
,
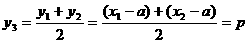 . ……10分
. ……10分
∴ 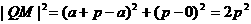 .
.
又 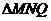 为等腰直角三角形,
为等腰直角三角形,
∴ 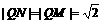 ,
,
∴ 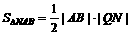 . ……12分
. ……12分
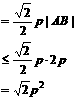
即 面积最大值为
面积最大值为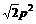 ……14分
……14分
(13)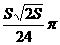 (14)
(14)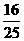 (15)
(15)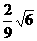 (16)②④
(16)②④
(1)A (2)C (3)D (4)C (5)A (6)B
(7)D (8)B (9)C (10)B (11)C (12)C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com