
题目列表(包括答案和解析)
6.已知 均为锐角,若
均为锐角,若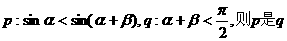 的 ( )
的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解:∵由 、
、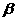 均为锐角,
均为锐角,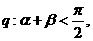 得0<α<α+β<
得0<α<α+β<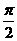 ∴sin(α+β)>sinα,但
∴sin(α+β)>sinα,但 、
、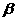 均为锐角,sinα<sin(α+β),不一定能推出α+β<
均为锐角,sinα<sin(α+β),不一定能推出α+β<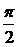 ,如α=
,如α=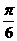 ,β=
,β=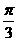 就是一个反例,选(C)
就是一个反例,选(C)
5.不等式组 的解集为 ( )
的解集为 ( )
A.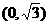 B.
B.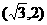 C.
C.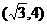 D.
D.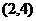
解∵|x-2|<2的解集为(0,4),log2(x2-1)>1的解集为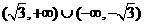 ,∴不等式组
,∴不等式组 的解集
的解集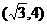 ,选(C)
,选(C)
4.设向量a=(-1,2),b=(2,-1),则(a·b)(a+b)等于 ( )
A.(1,1) B.(-4,-4) C.-4 D.(-2,-2)
解:(a·b)(a+b)=[-2+(-2)](1,1)=(-4,-4),选(B)
3.若函数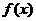 是定义在R上的偶函数,在
是定义在R上的偶函数,在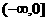 上是减函数,且
上是减函数,且 ,则使得
,则使得
 的取值范围是 ( )
的取值范围是 ( )
A. B.
B.
C. D.(-2,2)
D.(-2,2)
解:∵函数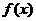 是定义在R上的偶函数,在
是定义在R上的偶函数,在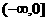 上是减函数,且
上是减函数,且 ,∴f(-2)=0, 在
,∴f(-2)=0, 在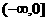 上
上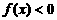 的x的取值范围是
的x的取值范围是 ,又由对称性
,又由对称性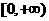 ,∴在R上fx)<0仰x的取值范围为(-2,2),选(D)
,∴在R上fx)<0仰x的取值范围为(-2,2),选(D)
2.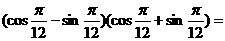 ( )
( )
A.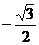 B.
B.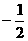 C.
C.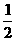 D.
D.
解: ,选(D)
,选(D)
1.圆 关于原点(0,0)对称的圆的方程为 ( )
关于原点(0,0)对称的圆的方程为 ( )
A. B.
B.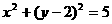
C. D.
D.
解:∵圆 的圆心(-2,0)关于原点对称的点为(2,0),∴圆
的圆心(-2,0)关于原点对称的点为(2,0),∴圆 关于原点对称的圆为(x-2)2+y2=5,选(A).
关于原点对称的圆为(x-2)2+y2=5,选(A).
22.(本小题12分)
(Ⅰ)证明:(1)当n=2时, ,不等式成立.
,不等式成立.
(2)假设当 时不等式成立,即
时不等式成立,即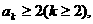
那么 . 这就是说,当
. 这就是说,当 时不等式成立.
时不等式成立.
根据(1)、(2)可知: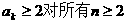 成立.
成立.
(Ⅱ)证法一:
由递推公式及(Ⅰ)的结论有

两边取对数并利用已知不等式得
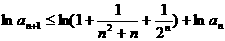
 故
故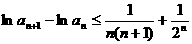
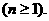
上式从1到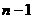 求和可得
求和可得


即
(Ⅱ)证法二:
由数学归纳法易证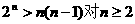 成立,故
成立,故

令
取对数并利用已知不等式得 

上式从2到n求和得 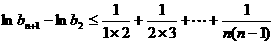

因
故 成立.
成立.
21.(本小题12分)
解:(Ⅰ)设双曲线C2的方程为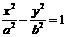 ,则
,则
故C2的方程为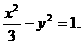
(II)将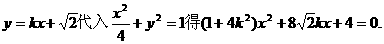
由直线l与椭圆C1恒有两个不同的交点得
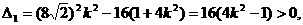
即 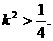 ①
①
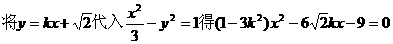 .
.
由直线l与双曲线C2恒有两个不同的交点A,B得


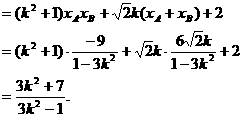
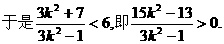 解此不等式得
解此不等式得
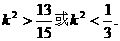 ③
③
由①、②、③得

故k的取值范围为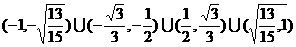
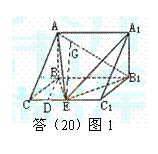
20.(本小题13分)
解法一:
(Ⅰ)因AB⊥面BB1C1C,故AB⊥BE.
又EB1⊥EA,且EA在面BCC1B1内的射影为EB.
由三垂线定理的逆定理知EB1⊥BE,因此BE是异面直线
AB与EB1的公垂线,
在平行四边形BCC1B1中,设EB=x,则EB1=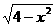 ,
,
作BD⊥CC1,交CC1于D,则BD=BC·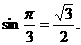
在△BEB1中,由面积关系得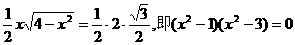 .
.
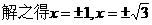 (负根舍去)
(负根舍去)

解之得CE=2,故此时E与C1重合,由题意舍去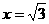 .
.
因此x=1,即异面直线AB与EB1的距离为1.
(Ⅱ)过E作EG//B1A1,则GE⊥面BCC1B,故GE⊥EB1且GE在圆A1B1E内,
又已知AE⊥EB1
故∠AEG是二面角A-EB1-A1的平面角.
因EG//B1A1//BA,∠AEG=∠BAE,故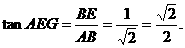
解法二:
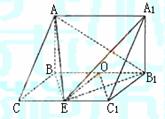 (Ⅰ)
(Ⅰ)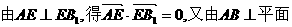
而BB1C1C得AB⊥EB1从而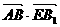 =0.
=0.
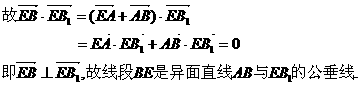
设O是BB1的中点,连接EO及OC1,则在Rt△BEB1中,EO=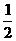 BB1=OB1=1,
BB1=OB1=1,
因为在△OB1C1中,B1C1=1,∠OB1C1=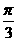 ,故△OB1C1是正三角形,
,故△OB1C1是正三角形,
所以OC1=OB1=1,
又因∠OC1E=∠B1C1C-∠B1C1O=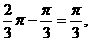 故△OC1E是正三角形,
故△OC1E是正三角形,
所以C1E=1,故CE=1,易见△BCE是正三角形,从面BE=1,
即异面直线AB与EB1的距离是1.
(Ⅱ)由(I)可得∠AEB是二面角A-EB1-B的平面角,在Rt△ABE中,由AB=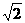 ,
,
BE=1,得tanAEB=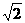 .
.
又由已知得平面A1B1E⊥平面BB1C1C,
故二面角A-EB1-A1的平面角 ,故
,故

解法三:
(I)以B为原点, 、
、 分别为y、z轴建立空间直角坐标系.
分别为y、z轴建立空间直角坐标系.
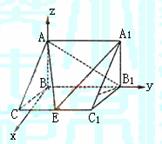 由于BC=1,BB1=2,AB=
由于BC=1,BB1=2,AB=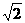 ,∠BCC1=
,∠BCC1=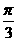 ,
,
在三棱柱ABC-A1B1C1中有
B(0,0,0),A(0,0,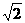 ),B1(0,2,0),
),B1(0,2,0),
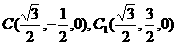
设

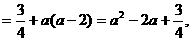
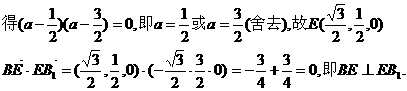
又AB⊥面BCC1B1,故AB⊥BE. 因此BE是异面直线AB、EB1的公垂线,
则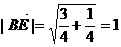 ,故异面直线AB、EB1的距离为1.
,故异面直线AB、EB1的距离为1.
(II)由已知有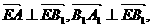 故二面角A-EB1-A1的平面角
故二面角A-EB1-A1的平面角 的大小为向量
的大小为向量
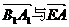 的夹角.
的夹角.

19.(本小题13分)

(1)当
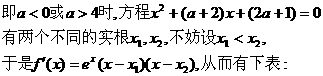
|
x |
 |
x1 |
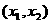 |
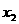 |
 |
 |
+ |
0 |
- |
0 |
+ |
 |
 |
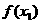 为极大值 为极大值 |
 |
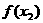 为极小值 为极小值 |
 |
即此时 有两个极值点.
有两个极值点.
(2)当 有两个相同的实根
有两个相同的实根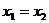
于是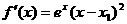
 无极值.
无极值.
(3)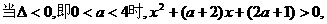
 为增函数,此时
为增函数,此时 无极值. 因此当
无极值. 因此当 无极值点.
无极值点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com