
题目列表(包括答案和解析)
18、(本小题满分12分)
某商场举行抽奖促销活动,抽奖规则是:从装有9个白球,1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球可获得奖金10元;摸出2个红球可获得奖金50元,现有甲,乙两位顾客,规定:甲摸一次,乙摸两次,令x表示甲,乙摸球后获得的奖金总额。求:
(1)x的分布列 (2)x的的数学期望
17、解:(1)f(x)=x3+ax2+bx+c,f¢(x)=3x2+2ax+b
由f¢(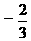 )=
)=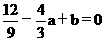 ,f¢(1)=3+2a+b=0得
,f¢(1)=3+2a+b=0得
a=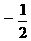 ,b=-2
,b=-2
f¢(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
|
x |
(-¥,- ) ) |
- |
(- ,1) ,1) |
1 |
(1,+¥) |
|
f¢(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
¯ |
极小值 |
|
所以函数f(x)的递增区间是(-¥,- )与(1,+¥)
)与(1,+¥)
递减区间是(- ,1)
,1)
(2)f(x)=x3-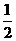 x2-2x+c,xÎ(-1,2),当x=-
x2-2x+c,xÎ(-1,2),当x=- 时,f(x)=
时,f(x)=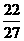 +c
+c
为极大值,而f(2)=2+c,则f(2)=2+c为最大值。
要使f(x)<c2(xÎ(-1,2))恒成立,只需c2>f(2)=2+c
解得c<-1或c>2
17、(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c在x=- 与x=1时都取得极值
与x=1时都取得极值
(3) 求a、b的值与函数f(x)的单调区间
(4) 若对xÎ(-1,2),不等式f(x)<c2恒成立,求c的取值范围。
16、已知圆M:(x+cosq)2+(y-sinq)2=1,
 直线l:y=kx,下面四个命题:
直线l:y=kx,下面四个命题:
(D) 对任意实数k与q,直线l和圆M相切;
(E) 对任意实数k与q,直线l和圆M有公共点;
(F) 对任意实数q,必存在实数k,使得直线l与
和圆M相切
(D)对任意实数k,必存在实数q,使得直线l与
和圆M相切
其中真命题的代号是______________(写出所有真命题的代号)
解:圆心坐标为(-cosq,sinq)d=
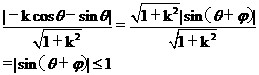
故选(B)(D)
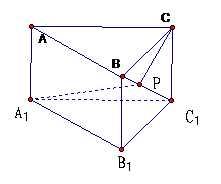
15、如图,在直三棱柱ABC-A1B1C1中,底面为直角三角形,ÐACB=90°,AC=6,BC=CC1=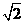 ,P是BC1上一动点,则CP+PA1的最小值是___________
,P是BC1上一动点,则CP+PA1的最小值是___________
解:连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,如图所示,
|
|

|
|


 连A1C,则A1C的长度就是所求的最小值。
连A1C,则A1C的长度就是所求的最小值。
通过计算可得ÐA1C1C=90°又ÐBC1C=45°
\ÐA1C1C=135° 由余弦定理可求得A1C=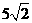
14、设f(x)=log3(x+6)的反函数为f-1(x),若(f-1(m)+6)(f-1(n)+6)=27
则f(m+n)=___________________
解:f-1(x)=3x-6故(f-1(m)+6)·(f-1(x)+6)=3m·3n=3m +n=27
\m+n=3\f(m+n)=log3(3+6)=2
13、解: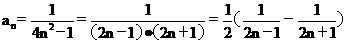
故
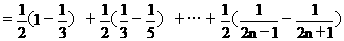
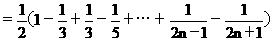
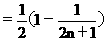
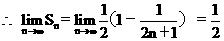
13、数列{ }的前n项和为Sn,则
}的前n项和为Sn,则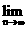 Sn=
Sn=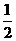
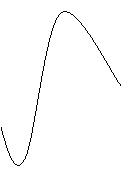
12、某地一年的气温Q(t)(单位:ºc)与时间t(月份)之间的关系如图(1)所示,已知该年的平均气温为10ºc,令G(t)表示时间段(0,t)的平均气温,G(t)与t之间的函数关系用下列图象表示,则正确的应该是( A )
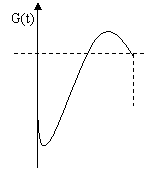
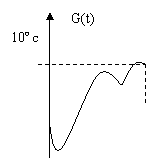
|
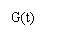
|
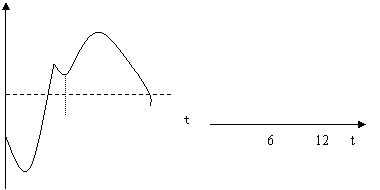

|
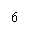
|


|
|
|
|
|
|
|||
|
|||
|
|

|
|
|
|
|

|
|
|
|

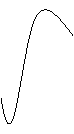
|

|

|


解:结合平均数的定义用排除法求解
理科数学
第Ⅱ卷(非选择题 共90分)
请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效。
11、如图,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1,S2,则必有( )
A. S1<S2
B. S1>S2
C. 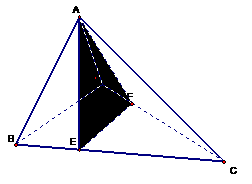 S1=S2
S1=S2
D. S1,S2的大小关系不能确定
解:连OA、OB、OC、OD
则VA-BEFD=VO-ABD+VO-ABE+VO-BEFD
VA-EFC=VO-ADC+VO-AEC+VO-EFC又VA-BEFD=VA-EFC而每个三棱锥的高都是原四面体的内切球的半径,故SABD+SABE+SBEFD=SADC+SAEC+SEFC又面AEF公共,故选C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com