
题目列表(包括答案和解析)
2.设复数: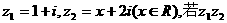 为实数,则x= ( )
为实数,则x= ( )
A.-2 B.-1 C.1 D.2
[思路点拨]本题考察复数的乘法运算,可直接计算得到答案.
[正确解答]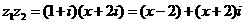 为实数,故
为实数,故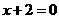 ,即
,即 .选A.
.选A.
[解后反思]复数有两个部分:实部和虚部.而且复数的几种代数运算,其基本算法也是尽可能将其化成复数的代数形式.
1.设集合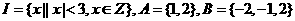 ,则
,则 ( )
( )
A.{1} B.{1,2} C.{2} D.{0,1,2}
[思路点拨]本题考察集合的逻辑运算,可直接求得.
[正确解答]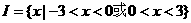 ,
,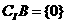 ,
,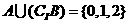 .选D.
.选D.
[解后反思]集合主要有三种逻辑运算:交集,并集,补集,运算时要留意集合元素的性质,元素确定性,互异性,无序性,要注意补集的运算是离不开全集的,在化简集合时,经常用到两种工具:数轴和韦恩图.
(1) 设集合A={1,2},B={1,2,3},C={2,3,4},则
(A){1,2,3} (B){1,2,4} (C){2,3,4} (D){1,2,3,4}
(2) 函数 的反函数的解析表达式为
的反函数的解析表达式为
(A) (B)
(B)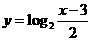
(C) (D)
(D)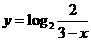
(3) 在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+a4+a5=
(A)33 (B)72 (C)84 (D)189
(4) 在正三棱柱ABC-A1B1C1中,若AB=2,AA1=1则点A到平面A1BC的距离为
(A)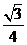 (B)
(B)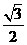 (C)
(C)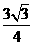 (D)
(D)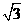
(5) △ABC中,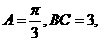 则△ABC的周长为
则△ABC的周长为
(A)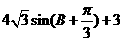 (B)
(B)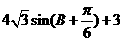
(C)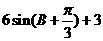 (D)
(D)
(6) 抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标是
(A)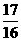 (B)
(B)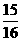 (C)
(C)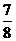 (D)0
(D)0
(7) 在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
9.4 8.4 9.4 9.9 9.6 9.4 9.7
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
(A)9.4, 0.484 (B)9.4, 0.016 (C)9.5, 0.04 (D)9.5, 0.016
(8) 设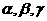 为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
①若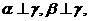 则
则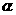 ∥
∥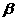 ;
;
②若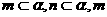 ∥
∥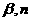 ∥
∥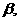 则
则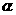 ∥
∥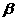 ;
;
③若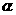 ∥
∥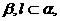 则
则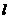 ∥
∥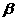 ;
;
④若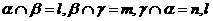 ∥
∥ 则m∥n.
则m∥n.
其中真命题的个数是
(A)1 (B)2 (C)3 (D)4
(9) 设k=1,2,3,4,5,则(x+2)5的展开式中xk的系数不可能是
(A)10 (B)40 (C)50 (D)80
(10) 若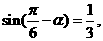 则
则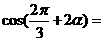
(A)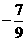 (B)
(B)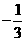 (C)
(C)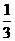 (D)
(D)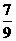
(11) 点P(-3,1)在椭圆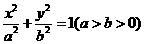 的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为
的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为
(A)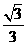 (B)
(B)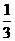 (C)
(C)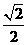 (D)
(D)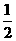
(12) 四棱锥的8条棱代表8种不同的化工产品,有公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共顶点的两条棱代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,那么安全存放的不同方法种数为
(A)96 (B)48 (C)24 (D)0
21.(本小题满分14分)
已知椭圆C: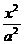 +
+ =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线
l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设 =λ
=λ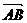 .
.
(Ⅰ)证明:λ=1-e2;
(Ⅱ)若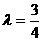 ,△PF1F2的周长为6;写出椭圆C的方程;
,△PF1F2的周长为6;写出椭圆C的方程;
(Ⅲ)确定λ的值,使得△PF1F2是等腰三角形.
2005年普通高等学校招生全国统一考试(湖南卷)
20.(本小题满分14分)
某单位组织4个部门的职工旅游,规定每个部门只能在韶山、衡山、张家界3个景区中任选一个,假设各部门选择每个景区是等可能的.
(Ⅰ)求3个景区都有部门选择的概率;
(Ⅱ)求恰有2个景区有部门选择的概率.
19.(本小题满分14分)
设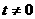 ,点P(
,点P(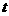 ,0)是函数
,0)是函数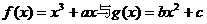 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用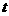 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求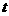 的取值范围.
的取值范围.
18.(本小题满分14分)
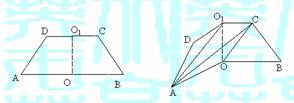 如图1,已知ABCD是上.下底边长分别为2和6,高为
如图1,已知ABCD是上.下底边长分别为2和6,高为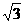 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求二面角O-AC-O1的大小.
|
17.(本小题满分12分)
已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
16.(本小题满分12分)
已知数列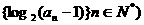 为等差数列,且
为等差数列,且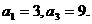
(Ⅰ)求数列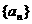 的通项公式;
的通项公式;
(Ⅱ)证明
15.已知平面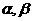 和直线,给出条件:①
和直线,给出条件:①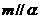 ;②
;②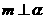 ;③
;③ ;④
;④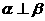 ;⑤
;⑤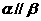 .
.
(i)当满足条件
时,有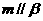 ;(ii)当满足条件
时,有
;(ii)当满足条件
时,有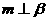 .
.
(填所选条件的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com