
题目列表(包括答案和解析)
22、(本题满分18分)对定义域是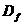 、
、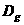 的函数
的函数 、
、 ,规定:函数
,规定:函数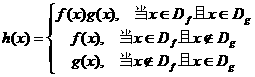 .
.
(1)若函数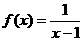 ,
,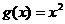 ,写出函数
,写出函数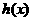 的解析式;
的解析式;
(2)求问题(1)中函数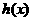 的值域;
的值域;
(3)若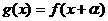 ,其中
,其中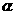 是常数,且
是常数,且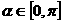 ,请设计一个定义域为R的函数
,请设计一个定义域为R的函数 ,及一个
,及一个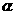 的值,使得
的值,使得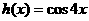 ,并予以证明.
,并予以证明.
见理21
21、(本题满分16分)已知抛物线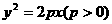 的焦点为F,A是抛物线上横坐标为4、且位于
的焦点为F,A是抛物线上横坐标为4、且位于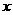 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于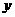 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作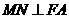 ,垂足为N,求点N的坐标;
,垂足为N,求点N的坐标;
(3)以M为圆心,MB为半径作圆M,当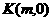 是
是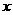 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.
[思路点拨]本题考查直线与抛物线、直线与圆的位置关系等基础知识,考查运用解析几何的方法分析问和解决问题的能力.第(1)(2)问是定量分析,难度不大,而解决(3)的常规方法之一就是利用点M到直线AK的距离d与圆的半径比较为宜.
[正确解答] (1) 抛物线y2=2px的准线为x=-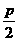 ,于是4+
,于是4+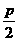 =5, ∴p=2.
=5, ∴p=2.
∴抛物线方程为y2=4x.
(2)∵点A是坐标是(4,4), 由题意得B(0,4),M(0,2),
又∵F(1,0), ∴kFA=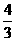 ;MN⊥FA, ∴kMN=-
;MN⊥FA, ∴kMN=-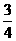 ,
,
则FA的方程为y=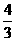 (x-1),MN的方程为y-2=-
(x-1),MN的方程为y-2=-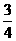 x,解方程组得x=
x,解方程组得x=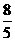 ,y=
,y=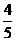 ,
,
∴N的坐标(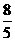 ,
,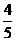 ).
).
(1) 由题意得, ,圆M.的圆心是点(0,2), 半径为2,
当m=4时, 直线AK的方程为x=4,此时,直线AK与圆M相离.
当m≠4时, 直线AK的方程为y=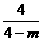 (x-m),即为4x-(4-m)y-4m=0,
(x-m),即为4x-(4-m)y-4m=0,
圆心M(0,2)到直线AK的距离d=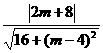 ,令d>2,解得m>1
,令d>2,解得m>1
∴当m>1时, AK与圆M相离;
当m=1时, AK与圆M相切;
当m<1时, AK与圆M相交.
[解后反思]解答圆锥这部分试题需准确地把握数与形的语言转换能力,推理能力,本题计算量并不大,但步步等价转换的意识要准确无误.
20、(本题满分14分)假设某市2004年新建住房面积400万平方米,其中有250万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,
(1)该市历年所建中低价层的累计面积(以2004年为累计的第一年)将首次不少于4780万平方米?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?
见理20
19、(本题满分14分)已知函数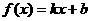 的图象与
的图象与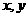 轴分别相交于点A、B,
轴分别相交于点A、B,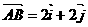 (
(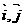 分别是与
分别是与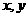 轴正半轴同方向的单位向量),函数
轴正半轴同方向的单位向量),函数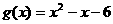 .
.
(1)求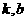 的值;
的值;
(2)当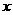 满足
满足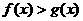 时,求函数
时,求函数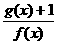 的最小值.
的最小值.
[思路点拨]本题是以向量为背景,解析法为手段,考查解析思想的运用和处理函数性质的方法,考查运算能力和运用数学模型的能力.
[正确解答] (1)由已知得A(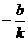 ,0),B(0,b),则
,0),B(0,b),则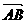 ={
={ ,b},于是
,b},于是 =2,b=2. ∴k=1,b=2.
=2,b=2. ∴k=1,b=2.
(2)由f(x)> g(x),得x+2>x2-x-6,即(x+2)(x-4)<0, 得-2<x<4,
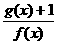 =
=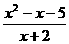 =x+2+
=x+2+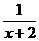 -5
-5
由于x+2>0,则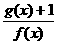 ≥-3,其中等号当且仅当x+2=1,即x=-1时成立
≥-3,其中等号当且仅当x+2=1,即x=-1时成立
∴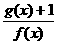 的最小值是-3.
的最小值是-3.
[解后反思]要熟悉在其函数的定义域内,常见模型函数求最值的常规方法.如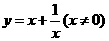 型.
型.
18、(本题满分12分)在复数范围内解方程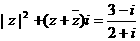 (
(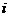 为虚数单位).
为虚数单位).
[思路点拨]见理18.
[正确解答]原方程化简为 ,
,
设z=x+yi(x、y∈R),代入上述方程得 x2+y2+2xi=1-i,
∴x2+y2=1且2x=-1,解得x=-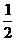 且y=±
且y=±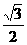 ,
,
∴原方程的解是z=-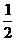 ±
±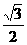 i.
i.
[解后反思]见理18.
17、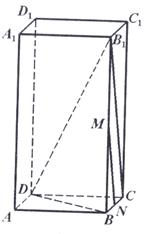 (本题满分12分)已知长方体
(本题满分12分)已知长方体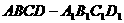 中,M、N分别是
中,M、N分别是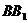 和BC的中点,AB=4,AD=2,
和BC的中点,AB=4,AD=2,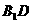 与平面ABCD所成角的大小为
与平面ABCD所成角的大小为 ,求异面直线
,求异面直线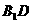 与MN所成角的大小.(结果用反三角函数值表示)
与MN所成角的大小.(结果用反三角函数值表示)
[思路点拨]见理17.
[正确解答]联结B1C,由M、N分别是BB1和BC的中点,得B1C∥MN,
∴∠DB1C就是异面直线B1D与MN所成的角.
联结BD,在Rt△ABD中,可得BD=2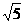 ,又BB1⊥平面ABCD, ∠B1DB是B1D与平面ABCD所成的角, ∴∠B1DB=60°.
,又BB1⊥平面ABCD, ∠B1DB是B1D与平面ABCD所成的角, ∴∠B1DB=60°.
在Rt△B1BD中, B1B=BDtan60°=2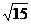 ,
,
又DC⊥平面BB1C1C, ∴DC⊥B1C,
在Rt△DB1C中, tan∠DB1C= ,
,
∴∠DB1C=arctan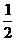 .
.
即异面直线B1D与MN所成角的大小为arctan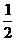 .
.
[解后反思]见理17.
16、 用
用 个不同的实数
个不同的实数 可得到
可得到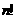 个不同的排列,每个排列为一行写成一个
个不同的排列,每个排列为一行写成一个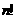 行的数阵.对第
行的数阵.对第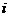 行
行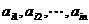 ,记
,记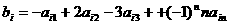 ,
,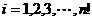 .例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以,
.例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以, ,那么,在用1,2,3,4,5形成的数阵中,
,那么,在用1,2,3,4,5形成的数阵中,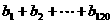 等于( )
等于( )
A.-3600 B.1800 C.-1080 D.-720
见理12
15、条件甲:“ ”是条件乙:“
”是条件乙:“ ”的( )
”的( )
A.既不充分也不必要条件B.充要条件 C.充分不必要条件 D.必要不充分条件
[思路点拨]本题考查了充要条件的定义及其判定只要判断甲 乙和乙
乙和乙 甲的真假性,利用充要条件将条件乙进行化简是解决这类问题的关键.
甲的真假性,利用充要条件将条件乙进行化简是解决这类问题的关键.
[正确解答]解法1:甲 乙:
乙: ,
,
乙 甲:
甲:
因此是充要条件,选B
解法2:∵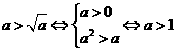 ,∴选B
,∴选B
[解后反思]对命题的充要条件、必要条件可以从三个方面理解:①定义法,②等价法,即利用 与
与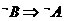 ,
,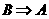 与
与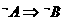 的等价关系,对于条件或结论是否定式的命题一般采用等价法,③利用集合间的包含关系判断:若
的等价关系,对于条件或结论是否定式的命题一般采用等价法,③利用集合间的包含关系判断:若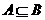 则A是B的充分条件或B是A必要条件;若
则A是B的充分条件或B是A必要条件;若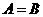 则A是B的充要条件,另外,对于确定条件的不充分性或不必要性往往用构造反例的方法来说明.
则A是B的充要条件,另外,对于确定条件的不充分性或不必要性往往用构造反例的方法来说明.
14、已知集合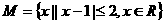 ,
,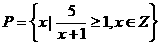 ,则
,则 等于( )
等于( )
A.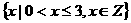 B.
B.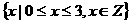
C.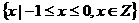 D.
D.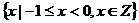
见理14.
13、若函数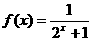 ,则该函数在
,则该函数在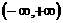 上是( )
上是( )
A.单调递减无最小值 B.单调递减有最小值
C.单调递增无最大值 D.单调递增有最大值
见理13
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com