
题目列表(包括答案和解析)
(1)已知平面向量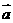 =(3,1),
=(3,1),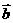 =(x,–3),且
=(x,–3),且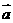 ⊥
⊥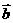 ,则x=
,则x=
(A) –3 (B) –1 (C) 1 (D)3
(2)已知A={x||2x+1|>3},B={x|x2+x≤6},则A∩B=
(A) (B)
(B)
(C)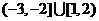 (D)
(D)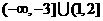
(3)设函数 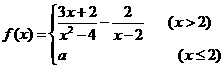 在x=2处连续,则a=
在x=2处连续,则a=
(A)-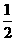 (B)-
(B)-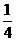 (C)
(C)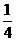 (D)
(D)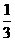
(4)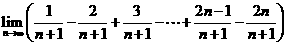 的值为
的值为
(A)–1 (B)0
(C)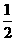 (D)1
(D)1
(5)函数f(x)=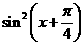 -
-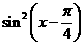 是
是
(A)周期为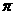 的偶函数
(B)周期为
的偶函数
(B)周期为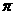 的奇函数
的奇函数
(C)周期为2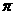 的偶函数
(D)周期为2
的偶函数
(D)周期为2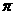 的奇函数
的奇函数
(6)一台X型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这种型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是
(A)0.1536 (B) 0.1808 (C) 0.5632 (D) 0.9728
(7)在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是
(A)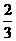 (B)
(B)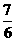 (C)
(C)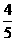 (D)
(D) 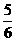
(8)若双曲线2x2-y2=k(k>0)的焦点到它相对应的准线的距离是2,则k=
(A) 6 (B) 8 (C) 1 (D) 4
(9)当0<x< 时,函数f(x)=
时,函数f(x)=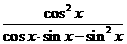 的最小值是
的最小值是
(A) 4
(B)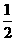 (C)2
(D)
(C)2
(D)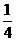
(10)变量x、y满足下列条件: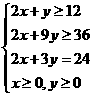 ,则使z=3x+2y的值最小的(x,y)是
,则使z=3x+2y的值最小的(x,y)是
(A)(4.5,3) (B)(3,6) (C)(9,2) (D)(6,4)
(11)若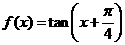 ,则
,则
(A)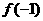 >
>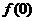 >
>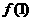 (B)
(B)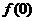 >
>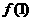 >
>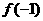
(C)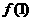 >
>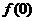 >
>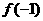 (D)
(D)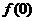 >
> 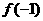 >
>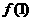
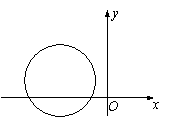 (12)如右下图,定圆半径为a,圆心为(b
,c),
则直线ax+by+c=0与直线 x–y+1=0的交点在
(12)如右下图,定圆半径为a,圆心为(b
,c),
则直线ax+by+c=0与直线 x–y+1=0的交点在
(A)第四象限
(B)第三象限
(C)第二象限
(D)第一象限
22.(本小题满分14分)
已知f(x)=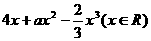 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=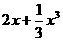 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
普通高等学校招生全国统一考试
21.(本小题满分12分)
如图,P是抛物线C:y=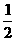 x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q.
(Ⅰ)当点P的横坐标为2时,求直线l的方程;
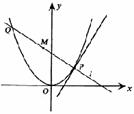 (Ⅱ)当点P在抛物线C上移动时,求线段PQ中点M的轨迹方程,并求点M到x轴的最短距离.
(Ⅱ)当点P在抛物线C上移动时,求线段PQ中点M的轨迹方程,并求点M到x轴的最短距离.
20.(本小题满分12分)
某企业2003年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+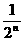 )万元(n为正整数).
)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
19.(本小题满分12分)
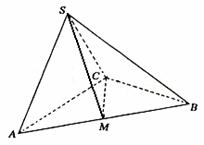 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2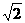 ,M为AB的中点.
,M为AB的中点.
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角S-CM-A的大小;
(Ⅲ)求点B到平面SCM的距离.
18.(本小题满分12分)
甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)分别求甲、乙两人考试合格的概率;
(Ⅱ)求甲、乙两人至少有一人考试合格的概率.
17.(本小题满分12分)
设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,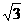 sin2x),x∈R.
sin2x),x∈R.
(Ⅰ)若f(x)=1-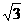 且x∈[-
且x∈[-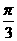 ,
,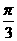 ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量c=(m,n)(|m|<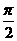 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
16.图1,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器(图2).当这个正六棱柱容器的底面边长为 时,其容积最大.
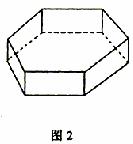
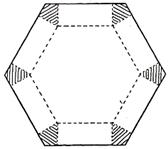
|
15.一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=6,则在第7组中抽取的号码是 .
14.设函数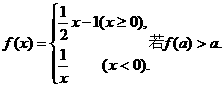 则实数a的取值范围是
.
则实数a的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com