
题目列表(包括答案和解析)
21.解:(I)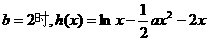 ,
,
则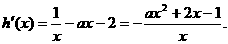
因为函数h(x)存在单调递减区间,所以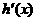 <0有解.
<0有解.
又因为x>0时,则ax2+2x-1>0有x>0的解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解;
则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0.
综上所述,a的取值范围为(-1,0)∪(0,+∞).
(II)证法一 设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为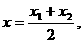
C1在点M处的切线斜率为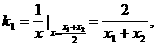
C2在点N处的切线斜率为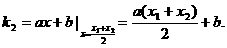
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2.
即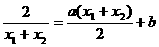 ,则
,则
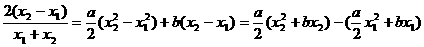
=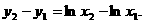
所以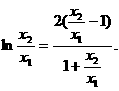 设
设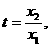 则
则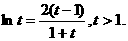 ①
①
令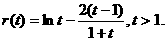 则
则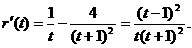
因为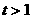 时,
时,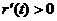 ,所以
,所以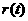 在
在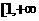 )上单调递增. 故
)上单调递增. 故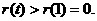
则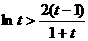 . 这与①矛盾,假设不成立.
. 这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
证法二:同证法一得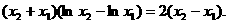
因为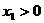 ,所以
,所以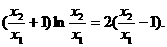
令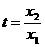 ,得
,得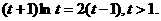 ②
②
令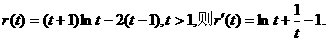
因为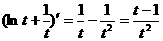 ,所以
,所以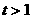 时,
时,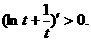
故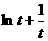 在[1,+
在[1,+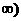 上单调递增.从而
上单调递增.从而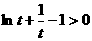 ,即
,即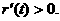
于是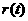 在[1,+
在[1,+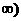 上单调递增.
上单调递增.
故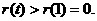 即
即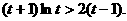 这与②矛盾,假设不成立.
这与②矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
20.解(I)从第n年初到第n+1年初,鱼群的繁殖量为axn,被捕捞量为bxn,死亡量为
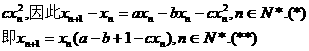
(II)若每年年初鱼群总量保持不变,则xn恒等于x1, n∈N*,从而由(*)式得
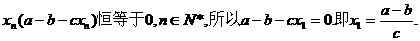
因为x1>0,所以a>b.
猜测:当且仅当a>b,且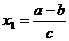 时,每年年初鱼群的总量保持不变.
时,每年年初鱼群的总量保持不变.
(Ⅲ)若b的值使得xn>0,n∈N*
由xn+1=xn(3-b-xn), n∈N*, 知
0<xn<3-b, n∈N*, 特别地,有0<x1<3-b. 即0<b<3-x1.
而x1∈(0, 2),所以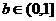
由此猜测b的最大允许值是1.
下证 当x1∈(0, 2) ,b=1时,都有xn∈(0, 2), n∈N*
①当n=1时,结论显然成立.
②假设当n=k时结论成立,即xk∈(0, 2),
则当n=k+1时,xk+1=xk(2-xk)>0.
又因为xk+1=xk(2-xk)=-(xk-1)2+1≤1<2,
所以xk+1∈(0, 2),故当n=k+1时结论也成立.
由①、②可知,对于任意的n∈N*,都有xn∈(0,2).
综上所述,为保证对任意x1∈(0, 2), 都有xn>0, n∈N*,则捕捞强度b的最大允许值是1.
19.(Ⅰ)证法一:因为A、B分别是直线l: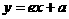 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是 .
.
所以点M的坐标是(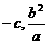 ). 由
). 由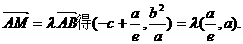
即
证法二:因为A、B分别是直线l: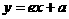 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是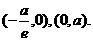 设M的坐标是
设M的坐标是
所以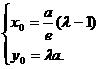 因为点M在椭圆上,所以
因为点M在椭圆上,所以 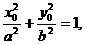
即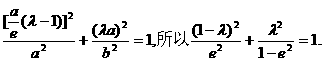
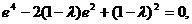 解得
解得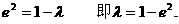
(Ⅱ)解法一:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即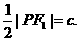
设点F1到l的距离为d,由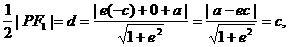
得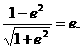 所以
所以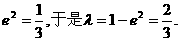
即当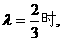 △PF1F2为等腰三角形.
△PF1F2为等腰三角形.
解法二:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,
设点P的坐标是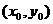 ,
,
则
由|PF1|=|F1F2|得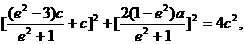
两边同时除以4a2,化简得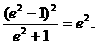 从而
从而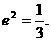
于是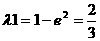 . 即当
. 即当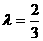 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.
18.解:(I)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”
为事件A1,A2,A3. 由已知A1,A2,A3相互独立,P(A1)=0.4,P(A2)=0.5,
P(A3)=0.6.
客人游览的景点数的可能取值为0,1,2,3. 相应地,客人没有游览的景点数的可能取
值为3,2,1,0,所以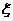 的可能取值为1,3.
的可能取值为1,3.
P(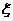 =3)=P(A1·A2·A3)+ P(
=3)=P(A1·A2·A3)+ P(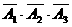 )
)
= P(A1)P(A2)P(A3)+P(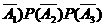 )
)
=2×0.4×0.5×0.6=0.24,
|
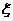 =1)=1-0.24=0.76.
=1)=1-0.24=0.76.
所以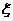 的分布列为
的分布列为
E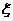 =1×0.76+3×0.24=1.48.
=1×0.76+3×0.24=1.48.
(Ⅱ)解法一 因为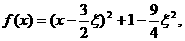
所以函数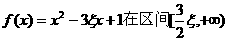 上单调递增,
上单调递增,
要使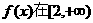 上单调递增,当且仅当
上单调递增,当且仅当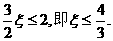
从而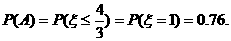
解法二: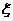 的可能取值为1,3.
的可能取值为1,3.
当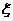 =1时,函数
=1时,函数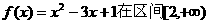 上单调递增,
上单调递增,
当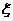 =3时,函数
=3时,函数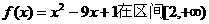 上不单调递增.0
上不单调递增.0
所以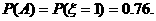
17. 解法一(I)证明 由题设知OA⊥OO1,OB⊥OO1.
解法一(I)证明 由题设知OA⊥OO1,OB⊥OO1.
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB. 故可以O为原点,OA、OB、OO1
所在直线分别为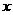 轴、y轴、z轴建立空间直角坐标系,
轴、y轴、z轴建立空间直角坐标系,
如图3,则相关各点的坐标是A(3,0,0),
B(0,3,0),C(0,1,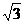 )
)
|
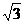 ).
).
从而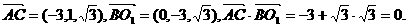
所以AC⊥BO1.
(II)解:因为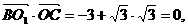 所以BO1⊥OC,
所以BO1⊥OC,
由(I)AC⊥BO1,所以BO1⊥平面OAC,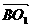 是平面OAC的一个法向量.
是平面OAC的一个法向量.
设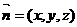 是0平面O1AC的一个法向量,
是0平面O1AC的一个法向量,
由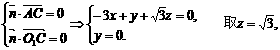 得
得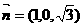 .
.
设二面角O-AC-O1的大小为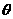 ,由
,由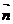 、
、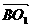 的方向可知
的方向可知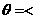
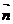 ,
,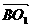 >,
>,
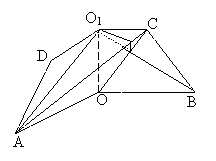 所以cos
所以cos
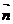 ,
,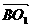 >=
>=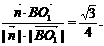
即二面角O-AC-O1的大小是
解法二(I)证明 由题设知OA⊥OO1,OB⊥OO1,
所以∠AOB是所折成的直二面角的平面角,
|
OC是AC在面OBCO1内的射影.
因为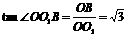
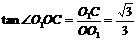 ,
,
所以∠OO1B=60°,∠O1OC=30°,从而OC⊥BO1
由三垂线定理得AC⊥BO1.
(II)解 由(I)AC⊥BO1,OC⊥BO1,知BO1⊥平面AOC.
设OC∩O1B=E,过点E作EF⊥AC于F,连结O1F(如图4),则EF是O1F在平面AOC
内的射影,由三垂线定理得O1F⊥AC.
所以∠O1FE是二面角O-AC-O1的平面角.
由题设知OA=3,OO1=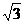 ,O1C=1,
,O1C=1,
所以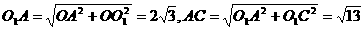 ,
,
从而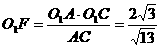 , 又O1E=OO1·sin30°=
, 又O1E=OO1·sin30°=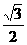 ,
,
所以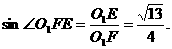 即二面角O-AC-O1的大小是
即二面角O-AC-O1的大小是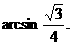
16.解法一 由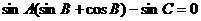
得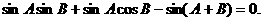
所以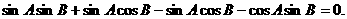
即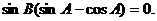
因为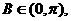 所以
所以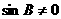 ,从而
,从而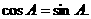
由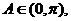 知
知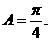 从而
从而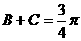 .
.
由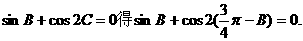
即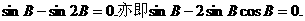
由此得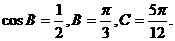 所以
所以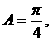
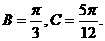
解法二:由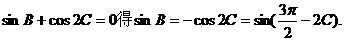
由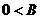 、
、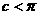 ,所以
,所以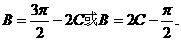
即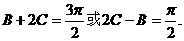
由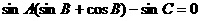 得
得 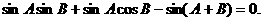
所以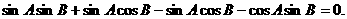
即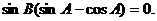 因为
因为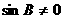 ,所以
,所以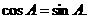
由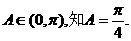 从而
从而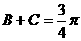 ,知B+2C=
,知B+2C=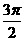 不合要求.
不合要求.
再由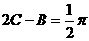 ,得
,得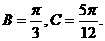 所以
所以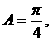
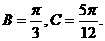
15.[答案]: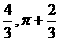
[解析]:本题是一道很好的理性思维信息开放性定义型题,能很好地考查学生分析思维能力.
由题意得: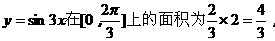
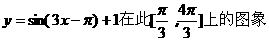
为一个半周期结合图象分析其面积为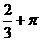 .
.
14.答案:-2
[解析]:由题意f(x)图象上点(4,0),关于(1,2)对称点(-2,4).则点(4,-2)在f--1(x)上,
则f--1(4)= -2.
13.答案: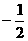
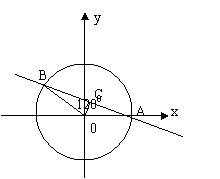 [解析]:如图
[解析]:如图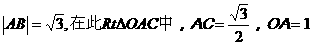
则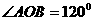
所以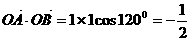 .
.
12.答案:35
[解析]:由题意得x2项的分数为: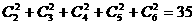 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com