
题目列表(包括答案和解析)
2、
已知圆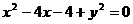 的圆心是点P,则点P到直线
的圆心是点P,则点P到直线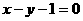 的距离是
的距离是 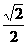 。
。
1、
已知集合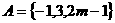 ,集合
,集合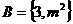 。若
。若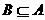 ,则实数
,则实数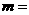
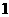 。
。
故f(α)=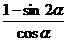 =
=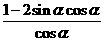 =
=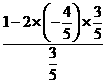 =
=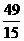 .
.
(16)(共13分)
解法一:
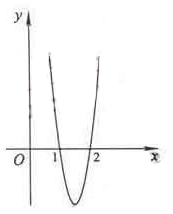
(Ⅰ)由图象可知,在(-∝,1)上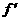 (x)>0,在(1,2)上
(x)>0,在(1,2)上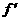 (x)<0.
在(2,+∝)上
(x)<0.
在(2,+∝)上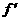 (x)>0.
(x)>0.
故f(x)在(-∝,1),(2,+∝)上递增,在(1,2)上递减.
因此f(x)在x=1处取得极大值,所以x0=1.
(Ⅱ) 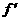 (x)=3ax2+2bx+c,
由
(x)=3ax2+2bx+c,
由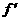 (1)=0,
(1)=0, 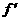 (2)=0, f(1)=5,
得
(2)=0, f(1)=5,
得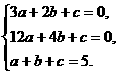 解得a=2,b=-9,c=12.
解法二:(Ⅰ)同解法一.
(Ⅱ)设
解得a=2,b=-9,c=12.
解法二:(Ⅰ)同解法一.
(Ⅱ)设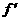 (x)=m(x-1)(x-2)=mx2-3mx+2m,
又
(x)=m(x-1)(x-2)=mx2-3mx+2m,
又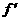 (x)=3ax2+2bx+c, 所以a=
(x)=3ax2+2bx+c, 所以a=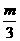 ,b=
,b=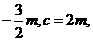
f(x)=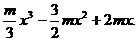 由f(l)=5, 即
由f(l)=5, 即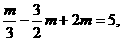 得m=6.
所以a=2,b=-9,c=12.
得m=6.
所以a=2,b=-9,c=12.
(17)(共14分)
解法一:
(Ⅰ)∵ABCD-A1B1C1D1是正四棱柱,∴CC1⊥平面ADCD, ∴BD⊥CC1
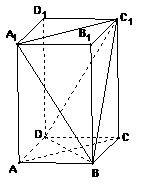 ∵ABCD是正方形 ∴BD⊥AC 又∵AC,CC1
∵ABCD是正方形 ∴BD⊥AC 又∵AC,CC1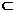 平面ACC1A1,
平面ACC1A1,
且AC∩CC1=C, ∴BD⊥平面ACC1A1.
(Ⅱ) 设BD与AC相交于O,连接C1O. ∵CC1⊥平面ADCD, ∴BD⊥AC,
∴BD⊥C1O, ∴∠C1OC∠是二面角C1-BD-C的平面角,
∴∠C1OC=60o. 连接A1B. ∵A1C1//AC, ∴∠A1C1B是BC1与AC所成的角.
设BC=a,则 ∴异面直线BC1与AC所成角的大小为
∴异面直线BC1与AC所成角的大小为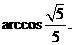
解法二:
(Ⅰ)建立空间直角坐标系D-xyz,如图.
设AD=a,DD1=b,则有D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),C1(0,a,b),
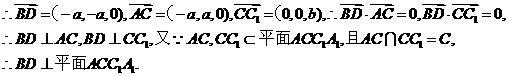
 (Ⅱ)设BD与AC相交于O,连接C1O,则点O坐标为
(Ⅱ)设BD与AC相交于O,连接C1O,则点O坐标为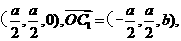
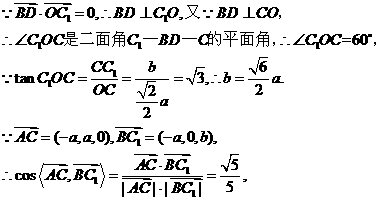 ∴异面直线BC1与AC所成角的大小为
∴异面直线BC1与AC所成角的大小为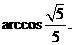
(18)(共13分)
解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,
则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(Ⅰ) 应聘者用方案一考试通过的概率
p1=P(A·B·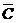 )+P(
)+P(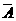 ·B·C)+P(A·
·B·C)+P(A·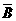 ·C)+P(A·B·C)
·C)+P(A·B·C)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9
=0.03+0.27+0.18+0.27
=0.75.
(Ⅱ) 应聘者用方案二考试通过的概率
p2=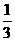 P(A·B)+
P(A·B)+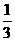 P(B·C)+
P(B·C)+ 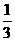 P(A·C)
P(A·C)
=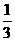 ×(0.5×0.6+0.6×0.9+0.5×0.9)
×(0.5×0.6+0.6×0.9+0.5×0.9)
=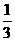 ×1.29
×1.29
=0.43
(19)(共14分)
解法一:
(Ⅰ)因为点P在椭圆C上,所以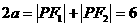 ,a=3.
,a=3.
在Rt△PF1F2中,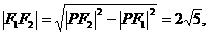 故椭圆的半焦距c=
故椭圆的半焦距c=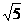 ,
,
从而b2=a2-c2=4,
所以椭圆C的方程为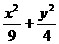 =1.
=1.
(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2).
已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
从而可设直线l的方程为
y=k(x+2)+1,
代入椭圆C的方程得
(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A,B关于点M对称.
所以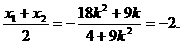
解得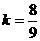 ,
,
所以直线l的方程为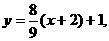
即8x-9y+25=0.
(经检验,所求直线方程符合题意)
解法二:
(Ⅰ)同解法一.
(Ⅱ)已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
设A,B的坐标分别为(x1,y1),(x2,y2).由题意x1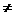 x2且
x2且
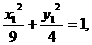 ①
①
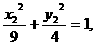 ②
②
由①-②得
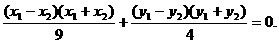 ③
③
因为A、B关于点M对称,
所以x1+ x2=-4, y1+ y2=2,
代入③得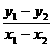 =
=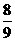 ,
,
即直线l的斜率为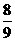 ,
,
所以直线l的方程为y-1=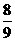 (x+2),
(x+2),
即8x-9y+25=0.
(经检验,所求直线方程符合题意.)
(20)(共14分)
解:(Ⅰ)由S14=98得2a1+13d=14,
又a11=a1+10d=0,
故解得d=-2,a1=20.
因此,{an}的通项公式是an=22-2n,n=1,2,3…
(Ⅱ)由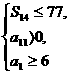 得
得 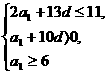 即
即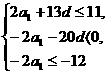
由①+②得-7d<11。
即d>-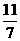 。
。
由①+③得13d≤-1
即d≤-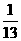
于是-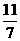 <d≤-
<d≤-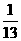
又d∈Z,故
d=-1
将④代入①②得10<a1≤12.
又a1∈Z,故a1=11或a1=12.
所以,所有可能的数列{an}的通项公式是
an=12-n和an=13-n,n=1,2,3,…
(14)
 (15)(本小题共12分)已知函数f(x)=
(15)(本小题共12分)已知函数f(x)=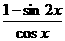 (Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tan
(Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tan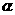 =
=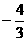 ,求f(
,求f(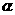 )的值.
)的值.
(16)(本小题共13分)
已知函数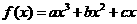 在点
在点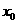 处取得极大值
处取得极大值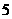 ,其导函数
,其导函数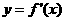 的图象经过点
的图象经过点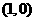 ,
,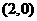 ,如图所示.求:
,如图所示.求:
(Ⅰ)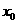 的值;
的值;
(Ⅱ)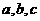 的值.
的值.
 (17)(本小题共14分)
(17)(本小题共14分)
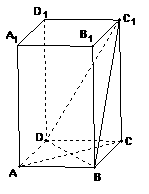
如图,ABCD-A1B1C1D1是正四棱柱.
(Ⅰ)求证:BD⊥平面ACC1A1;
(Ⅱ)]若二面角C1-BD-C的大小为60o,求异面直线BC1与AC所成角的大小.
(18)(本小题共13分)
某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
(19)(本小题共14分)
椭圆C: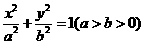 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且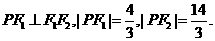
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l过圆x2+y2+4x-2y=0的圆心,交椭圆C于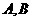 两点,且A、B关于点M对称,求直线l的方程.
两点,且A、B关于点M对称,求直线l的方程.
(20)(本小题共14分)
设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(Ⅰ)若a11=0,S14=98,求数列{an}的通项公式;
(Ⅱ)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式. 答案:
(9)若三点A(2,2),B(a,0),C(0,4)共线,则a的值等于 。
(10)在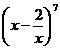 的展开式中,x3的系数是
.(用数字作答)
的展开式中,x3的系数是
.(用数字作答)
(11)已知函数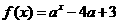 的反函数的图象经过点(-1,2),那么a的值等于 .
的反函数的图象经过点(-1,2),那么a的值等于 .
(12)已知向量a=(cos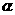 ,sin
,sin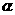 ),b=(cos
),b=(cos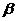 ,sin
,sin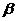 ),且a
),且a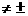 b,那么a+b与a-b的夹角的大小是
.
b,那么a+b与a-b的夹角的大小是
.
(13)在△ABC中,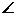 A,
A,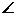 B,
B,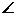 C所对的边长分别为a,b,c.若sinA:sinB:sinC=5∶7∶8,则a∶b∶c=
,
C所对的边长分别为a,b,c.若sinA:sinB:sinC=5∶7∶8,则a∶b∶c=
, 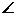 B的大小是 .
B的大小是 .
(14) 已知点P(x,y)的坐标满足条件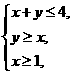 点O为坐标原点,那么|PO|的最小值等于____________,最大值等于______________.
点O为坐标原点,那么|PO|的最小值等于____________,最大值等于______________.
(1)设集合A=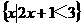 ,B=
,B=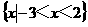 ,则A
,则A B等于
B等于
(A) 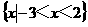 (B)
(B)
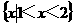 (C)
(C) 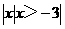 (D)
(D) 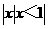
(2)函数y=1+cosx的图象
(A)关于x轴对称 (B)关于y轴对称
(C)关于原点对称 (D)关于直线x=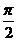 对称
对称
(3)若a与b-c都是非零向量,则“a·b=a·c”是“a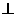 (b-c)”的
(b-c)”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D) 既不充分也不必要条件
(4)在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有
(A)36个 (B)24个 (C)18个 (D)6个
(5)已知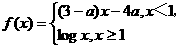 是(-
是(- ,+
,+ )上的增函数,那么a的取值范围是
)上的增函数,那么a的取值范围是
(A)(1,+ ) (B)(-
) (B)(- ,3)
(C)
,3)
(C)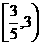 (D)(1,3)
(D)(1,3)
(6)如果-1,a,b,c,-9成等比数列,那么
(A)b=3,ac=9 (B)b=-3,ac=9 (C)b=3,ac=-9 (D)b=-3,ac=-9
(7)设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是
(A)若AC与BD共面,则AD与BC共面
(B)若AC与BD是异面直线,则AD与BC是异面直线
(C) 若AB=AC,DB=DC,则AD=BC
(D) 若AB=AC,DB=DC,则AD 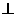 BC
BC
(8)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口A、B、C的机动车辆数如图所示,图中x1`x2`x3,分别表示该时段单位时间通过路段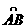 ,
,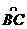 ,
,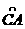 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A)x1>x2>x3 (B)x1>x3>x2
(C)x2>x3>x1 (D)x3>x2>x1
绝密★启用前
普通高等学校招生全国统一考试
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分。考试时间120分钟 考试结束,将本试卷和答题卡一并交回。
第Ⅱ卷(共110分)
1.用钢笔或圆珠笔将答案直接写在试卷上。
2.答卷前将密封线内的项目填写清楚。
(17)(本小题共12分)。
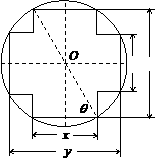
已知三棱锥P-ABC中,E、F分别是AC、AB的中点,
△ABC,△PEF都是正三角形,PF⊥AB.
(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P-AB-C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的球面上,
求△ABC的边长.
 ( 18 )(本小题共12分)
( 18 )(本小题共12分)
如图,在直径为1的圆 中,作一关于圆心对称、邻边互相
中,作一关于圆心对称、邻边互相
垂直的十字形,其中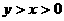 .
.
(Ⅰ)
将十字形的面积表示为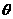 的函数;
的函数;
(Ⅱ)
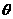 为何值时,十字形的面积最大?最大面积是多少?
为何值时,十字形的面积最大?最大面积是多少?
( 19 )(本小题共12分)
已知函数 .设数列
.设数列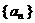 满足
满足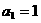 ,
,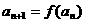 ,数列
,数列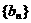 满足
满足
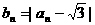 ,
,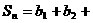 …
…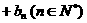 ,
,
(Ⅰ)用数学归纳法证明 ;(Ⅱ)证明
;(Ⅱ)证明 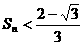 .
.
(20)(本小题满分12分)
某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
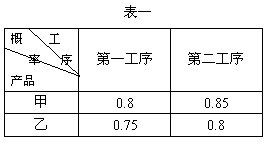 (Ⅰ)已知甲、乙两种产品每一道工序的
(Ⅰ)已知甲、乙两种产品每一道工序的
加工结果为A级的概率如表一所示,分别求生
产出的甲、乙产品为一等品的概率P甲、P乙;
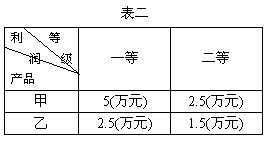 (Ⅱ)已知一件产品的利润如表二所示,用
(Ⅱ)已知一件产品的利润如表二所示,用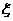 、
、
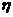 分别表示一件甲、乙产品的利润,在(Ⅰ)
分别表示一件甲、乙产品的利润,在(Ⅰ)
的条件下,求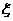 、
、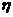 的分布列及
的分布列及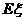 、
、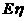 ;
;
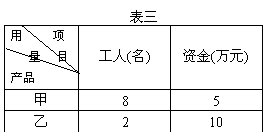 (Ⅲ)已知生产一件产品需用的工人数和资
(Ⅲ)已知生产一件产品需用的工人数和资
金如表三所示,该工厂有工人40名,可用资
金60万,设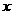 、
、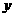 分别表示生产甲、乙产品
分别表示生产甲、乙产品
的数量,在(Ⅱ)的条件下,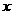 、
、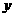 为何值时
为何值时
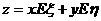 最大?最大值是多少?
最大?最大值是多少?
(解答时须给出图示)
 (21)(本小题满分14分)
(21)(本小题满分14分)
已知椭圆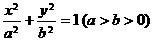 的左、右焦点分别是
的左、右焦点分别是
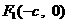 、
、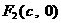 ,
,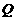 是椭圆外的动点,满足
是椭圆外的动点,满足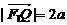 ,
,
点P是线段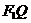 与该椭圆的交点,点T在线段
与该椭圆的交点,点T在线段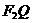 上,并且
上,并且
满足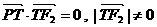 .
.
(Ⅰ)设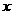 为点P的横坐标,证明
为点P的横坐标,证明 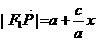 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△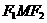 的面积
的面积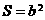 .若存在,求
.若存在,求
∠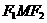 的正切值;若不存在,请说明理由.
的正切值;若不存在,请说明理由.
(22)(本小题满分12分)
函数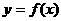 在区间
在区间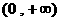 内可导,导函数
内可导,导函数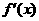 是减函数,且
是减函数,且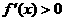 .设
.设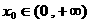 ,
,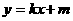 是曲线
是曲线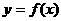 在点
在点 处的切线方程,并设函数
处的切线方程,并设函数
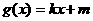 .
.
(Ⅰ)用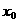 、
、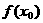 、
、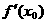 表示m;
表示m;
(Ⅱ)证明:当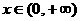 ,
,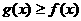 ;
;
(Ⅲ)若关于x的不等式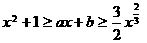 在
在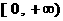 上恒成立,其中a、b为实数,求b的取值范围及a与b所满足的关系.
上恒成立,其中a、b为实数,求b的取值范围及a与b所满足的关系.
普通高等学校招生全国统一考试(辽宁卷)
(13)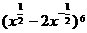 的展开式中常数项是______________.
的展开式中常数项是______________.
[答案]-160
 [解答]通项公式为
[解答]通项公式为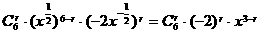 ,
,
由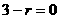 ,得
,得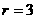 ,所以常数项是
,所以常数项是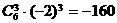 ,
,
[点拨]熟悉二项式展开式的通项公式.
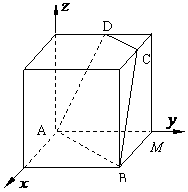
(14)如图,正方体的棱长为1,C、D分别是两条棱的中点,A、
B、M是顶点,那么点M到截面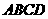 的距离是_____________.
的距离是_____________.
[答案]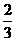
[解答]如图建立空间直角坐标系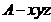 ,
,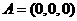 ,
,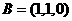 ,
,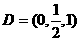 ,
,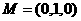 ,则
,则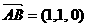 ,
,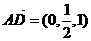 ,
,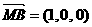 设
设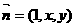 为平面
为平面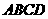 法向量,则有
法向量,则有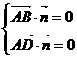 ,即
,即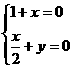 ,解得
,解得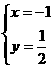 ,即
,即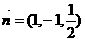 ,所以点M到截面
,所以点M到截面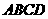 的距离
的距离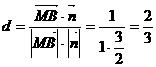 .
.
[点拨]利用法向量求点到平面的距离是较好操作的方法.
(15)用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1与2相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有___________个.(用数字作答)
[答案]576
[解答]将1与2,3与4,5与6捆绑在一起排成一列有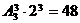 种,再将7、8插入4个空位中的两个有
种,再将7、8插入4个空位中的两个有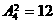 种,故有
种,故有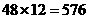 种.
种.
[点拨]相邻用捆绑法,不相邻用插空法
(16) 是正实数,设
是正实数,设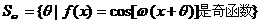 ,若对每个实数a ,
,若对每个实数a ,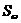 ∩
∩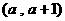 的元素不超过2个,且有a使
的元素不超过2个,且有a使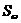 ∩
∩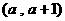 含有2个元素,则
含有2个元素,则 的取值范围是___________.
的取值范围是___________.
[答案]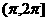
[解答]∵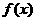 是奇函数,且
是奇函数,且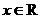 ,
,
∴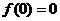 ,
,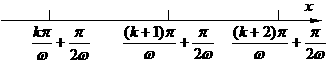 ∴
∴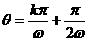 ,
,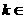 Z,
Z,
∵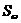 ∩
∩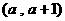 的元素不超过2个,
的元素不超过2个,
∴ ,∴
,∴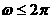 ,
,
∵且有a使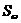 ∩
∩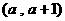 含有2个元素,
含有2个元素,
∴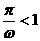 ,∴
,∴ ,∴
,∴ ,
,
[点拨]通过数轴得出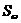 ∩
∩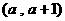 元素个数与两点间距离的关系再求解.
元素个数与两点间距离的关系再求解.
(1)数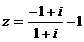 .在复平面内,z所对应的点在
(
)
.在复平面内,z所对应的点在
(
)
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
[答案]B
[解答]∵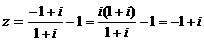
∴z所对应的点在第二象限.故选B.
[点拨]对于复数运算应先观察其特点再计算,会简化运算.
(2)极限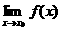 存在是函数
存在是函数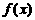 在点
在点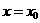 处连续的
( )
处连续的
( )
(A)充分而不必要的条件 (B)必要而不充分的条件
(C)充要条件 (D)既不充分也不必要的条件
[答案]B
[解答]∵极限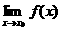 存在且
存在且 ,则函数
,则函数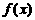 在点
在点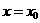 处连续的,
处连续的,
∴极限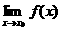 存在是函数
存在是函数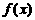 在点
在点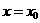 处连续的必要而不充分的条件,故选B.
处连续的必要而不充分的条件,故选B.
[点拨]准确理解函数连续性的概念及判断方法很重要.
(3)设袋中有80个红球,20个白球.若从袋中任取10个球,则其中恰有6个红球的概率为
(A)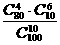 (B)
(B)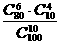 (C)
(C)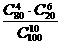 (D)
(D)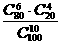
[答案]D
[解答]从袋中任取10个球有 种,其中恰有6个红球有
种,其中恰有6个红球有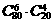 种,故选D.
种,故选D.
[点拨]分析如何完成取球任务,再利用组合计算.
(4)已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面.给出下列的四个命题:
①若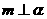 ,
,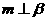 ,则
,则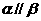 ;
;
②若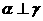 ,
,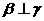 ,则
,则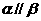 ;
;
③若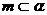 ,
,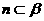 ,
,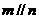 ,则
,则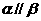 ;
;
④若m、n是异面直线,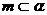 ,
,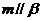 ,
,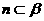 ,
,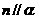 ,则
,则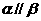 ,
,
其中真命题是
(A)①和② (B)①和③ (C)③和④ (D)①和④
[答案]D
[解答]因为垂直于同一条直线的两平面互相平行,所以①正确;因为垂直于同一平面的两平面不一定平行,所以②错误;因为当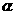 与
与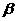 相交时,若m、n平行于两平面的交线,则
相交时,若m、n平行于两平面的交线,则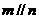 ,所以③错误;因为若m、n是异面直线,
,所以③错误;因为若m、n是异面直线,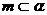 ,
,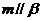 ,
,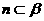 ,
,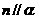 ,当且仅当
,当且仅当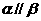 ,所以④正确.
,所以④正确.
[点拨]解立几推断题应联系具体图形以及相关定理解决.
(5)函数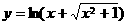 的反函数是
的反函数是
(A)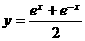 (B)
(B)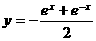 (C)
(C)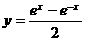 (D)
(D)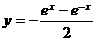
[答案]C
[解答]由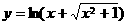 ,得
,得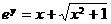 ,即
,即 ,
,
两边平方,化简得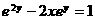 ,故
,故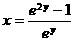 ,即
,即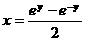 ,
,
∴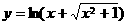 的反函数是
的反函数是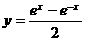 .
.
[点拨]求反函数设法解出x .
(6)若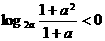 ,则a的取值范围是
,则a的取值范围是
(A)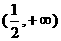 (B)
(B)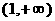 (C)
(C)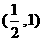 (D)
(D)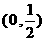
[答案]C
[解答]法一:代特殊值验证
法二:①当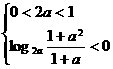 ,即
,即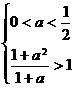 时,无解;
时,无解;
②当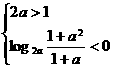 ,即
,即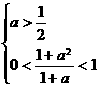 时,
时, ,故选C.
,故选C.
[点拨]解含参数对数不等式时,须注意分类讨论参数.
(7)在R上定义运算 :
: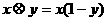 .若不等式
.若不等式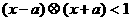 对任意实数x成立,则
对任意实数x成立,则
(A)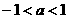 (B)
(B)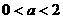 (C)
(C)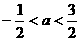 (D)
(D)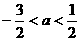
[答案]C
[解答]∵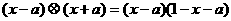 ,∴不等式
,∴不等式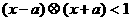 对任意实数x成立,则
对任意实数x成立,则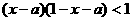 对任意实数x成立,即使
对任意实数x成立,即使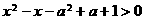 对任意实数x成立,所以
对任意实数x成立,所以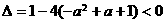 ,解得
,解得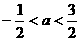 ,故选C.
,故选C.
[点拨]熟悉一元二次不等式恒成立与对应方程的判别式的关系.
(8)若钝角三角形三内角的度数成等差数列,且最大边与最小边长的比值为m,则m的范围是
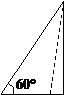 (A)
(A) (B)
(B)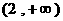 (C)
(C)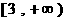 (D)
(D)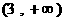
[答案]B
[解答]∵钝角三角形三内角的度数成等差数列,
∴其中一个角为60º,如图,直角三角形时,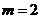 ,
,
所以钝角三角形时,有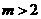 ,故选B.
,故选B.
[点拨]利用数形结合解题较快捷.
(9)若直线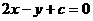 按向量
按向量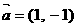 平移后与圆
平移后与圆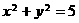 相切,则c的值为
相切,则c的值为
(A)8或-2 (B)6或-4 (C)4或-6 (D)2或-8
[答案]A
[解答]由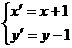 ,得
,得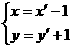 ,所以
,所以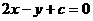 平移后,得
平移后,得 ,其与圆
,其与圆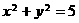 相切,即圆心到直线的距离为
相切,即圆心到直线的距离为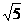 ,即
,即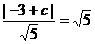 ,解得
,解得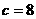 或
或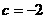 ,故选A.
,故选A.
[点拨]熟悉平移公式,直线与圆的位置关系应转化为圆心到直线的距离处理.
(10)已知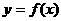 是定义在R上的单调函数,实数
是定义在R上的单调函数,实数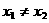 ,
,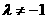 ,
,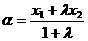 ,
,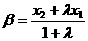 .若,则
.若,则
(A)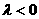 (B)
(B)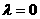 (C)
(C)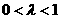 (D)
(D)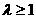
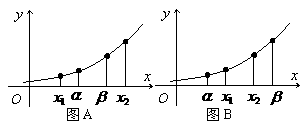 [答案]A
[答案]A
[解答]数形结合法:当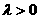 ,如图A所示,
,如图A所示,
有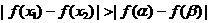 ,当
,当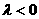 时,
时,
如图B所示,有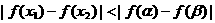 ,
,
故选A.
[点拨]数形结合解决定比分点问题.
(11)已知双曲线的中心在原点,离心率为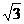 .若它的一条准线与抛物线
.若它的一条准线与抛物线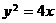 的准线重合,则
的准线重合,则
该双曲线与抛物线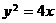 的交点到原点的距离是
的交点到原点的距离是
(A)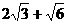 (B)
(B)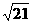 (C)
(C)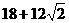 (D)21
(D)21
[答案]B
[解答]由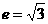 ,得
,得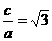 ,由一条准线与抛物线
,由一条准线与抛物线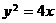 的准线重合,得准线为
的准线重合,得准线为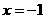 ,所以
,所以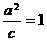 ,故
,故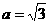 ,
,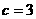 ,
,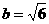 ,所以双曲线方程为
,所以双曲线方程为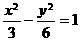 ,由
,由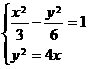 ,得交点为
,得交点为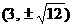 ,所以交点到原点的距离是
,所以交点到原点的距离是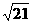 ,故选B.
,故选B.
[点拨]由已知条件发拨出a、b、c的取值,得到双曲线的方程.
(12)一给定函数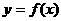 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意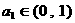 ,由关系式
,由关系式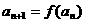
得到的数列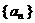 满足
满足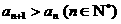 ,则该函数的图象是
,则该函数的图象是
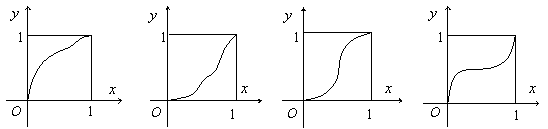
(A) (B) (C) (D)
[答案]A
[解答]由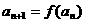 ,
,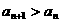 ,得
,得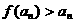 ,即
,即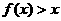 ,故选A .
,故选A .
[点拨]分析清楚函数值与自变量的关系,即可判断.
第Ⅱ卷 (非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com