
题目列表(包括答案和解析)
3.下列不等式中解集是Æ的是( )
A. 4x2-4x+1£0 B.4x2-4x-1£0
C. 4x2-4x+2£0 D.4x2-4x-2£0
2.关于x的不等式x2>a2与下列不等式中的( )等价.
A.x>a B.x>|a|
C.x>|a|或x<-|a| D.x>a或x<-a
1.下列不等式中,与不等式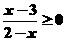 同解的是(
).
同解的是(
).
A.(x-3)(2-x)³0 B.(x-3)(2-x)>0
C.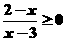 D.lg(x-2)£0
D.lg(x-2)£0
例1
已知全集I=R,集合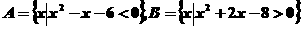 ,
,
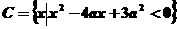 ,
,
(1)试求实数a的取值范围,使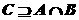 ;
;
(2)试求实数的取值范围,使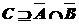 .
.
例2
解下列不等式: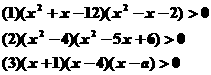
注意:这是一组解简单的高次不等式的问题,采用的解法叫做数轴标根法,图中所画的曲线实际上是函数f(x)=(x-x1)(x-x2)…(x-xn)的图象的示意图这一过程中,应当注意两点:(1)最右边的一个区间上,函数图象位于x轴的上方;(2)当相应的方程有偶次重根时,图像与x轴相切.
例3 设a¹b,解关于的不等式: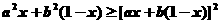
注意:解含字母系数的不等式,要有对字母作分类讨论的准备,但讨论什么,怎么讨论要在求解过程中看等价变形的要求去定,也可能不必讨论.
例4 解不等式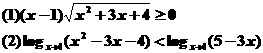
例5 解关于x的不等式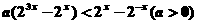
例6 解不等式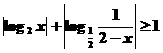
注意:化去不等式中的绝对值号转化为不含绝对值号的不等式是此类问题的通常思路,这就要确定log2x,log2(2-x)取正号或负号的条件,而其中对x作分类讨论的全集又是由x>0,且2-x>0,决定的.
例7
解关于x的不等式: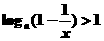
4、解简单的指数、对数不等式时,常用的方法有同底法、转化法、换元法和图象法等.
同底法:将指数、对数不等式转化为相同的底数后,再根据函数单调性进行同解变形。
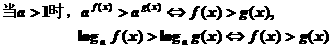
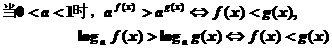
转化时,不要疏忽了对定义域的要求。
换元法:多用于两边是和的形式,把原不等式换元成一元二次不等式或无理不等式等形式,或先两边取对数后换元,要注意取对数时其数必须为正,要注意新元的取值范围.
转化法:多用于指数不等式,通常对不等式两边取同底对数,转化为对数不等式.要注意转化的等价性.
3、解含有绝对值符号的不等式关键是正确地脱去绝对值符号,转化为有理不等式再求解,常见的转化有:
(1)|f(x)|<g(x) (g(x)>0)Û-g(x)<f(x)<g(x)
(2) |f(x)|>g(x) (g(x)>0)Ûf(x)<-g(x)或f(x)>g(x)
(3) |f(x)|<|g(x)|Û f2(x)<g2(x)
或|f(x)|>|g(x)|Û [f(x)+g(x)][ f(x)-g(x)]>0
含有多个绝对值的不等式,可采用“零点分区间”法求解.利用绝对值的几何意义解含有绝对值符号的不等式,也是一种简便的方法.此外,借助函数图象也是一种好方法.
2、解无理不等式时,通常转化为有理不等式组求解.常见的转化有:
(1)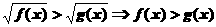
(2) 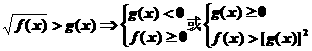
(3) 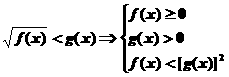
此外还可以通过换元法、图象法等.
不等式解法,包括一元一次不等式(组)、一元二次不等式(组)、分式不等式、高次不等式等有理不等式,简单的无理不等式、指数不等式、对数不等式以及含有绝对值符号的不等式的求解和解集的确定.
1、形如ax+b>0和ax2+bx+c>0(<0)(a¹0)的不等式(组)的解法和解集的确定要熟练掌握.它们是解各种类型不等式的基础.高次不等式的解法是通过因式分解,将它化为一次或二次因式的乘积,然后用“序轴标根法”求解集.解有理分式不等式时,一般先通过移项,把一边化为零,另一边化为因式之积或商,再等价转化为高次不等式解之.
(1)若a>b>c,则一定成立的不等式是( ).
(A)a|c|>b|c| (B)ab>ac
(C)a-|c|>b-|c| (D)a-|c|<b-|c|
(2)若x<a<0,则一定成立的不等式是( ).
(A)x2<ax<a2 (B)x2>ax>a2
(C)x2<a2<ax (D)x2>a2>ax
(3)a,bÎR,下列命题中的真命题是( ).
(A)若a>b,则|a|>|b| (B)若a>b,则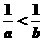
(C)若a>b,则a3>b3
(D)若a>b,则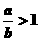
(4)设a,b是满足ab<0的实数,则( ).
(A)|a+b|<|a-b| (B)|a+b|>|a-b|
(C)|a-b|<||a|-|b|| (D)|a-b|<|a|+|b|
(5)以下四个不等式:¬a<0<b;b<a<0;® b<0<a;¯0<b<a,其中使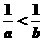 成立的充分条件有( ).
成立的充分条件有( ).
(A)1个 (B)2个 (C)3个 (D)4个
(6)已知a<b,化简|a-b-3|-|b-a+2|=_______
(7)已知a>b>c>d>0,且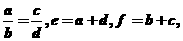 则e,f的大小关系是_____________
则e,f的大小关系是_____________
(8)已知 ,则a,b,0,1的大小顺序是________
,则a,b,0,1的大小顺序是________
(9)x>y或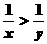 同时成立的充要条件是_______________
同时成立的充要条件是_______________
(10)已知a,b为不等正数,s<t<0,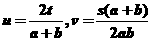 则u,v的大小关系是 ________________
则u,v的大小关系是 ________________
(11)已知-1<2a<0,将下列各数按照从小到大的顺序排列,并说明理由.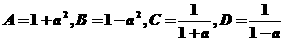
(12)已知a为正数,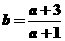 ,试比较
,试比较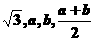 四个数的大小.
四个数的大小.
第二节 不等式的解法
例1 若a,b是任意实数,且a>b,则( ).
(A)a2>b2 (B)<1 (C)lg(a-b)>0 (D)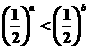
例2 已知都是实数,给出下列命题;
①ac2>bc2Ûa>b
②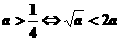
③(x-a)(x-b)£0Û
 ④
④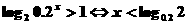
其中正确命题的个数是( ).
(A)1 (B)2 (C)3 (D)4
例3 设a,b是不相等的正数, 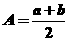 ,
,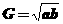 ,
,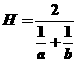 ,
,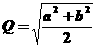 .试比较A、G、H、Q的大小.
.试比较A、G、H、Q的大小.
例4 船在流水中在甲地和乙地间来回行驶一次的平均速度和船在静水中的速度是否相等,为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com