
题目列表(包括答案和解析)
12.(浙江卷)“a>0,b>0”是“ab>0”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不允分也不必要条件
解:由“a>0,b>0”可推出“ab>0”,反之不一定成立,选A
11.(浙江卷)“a>b>c”是“ab<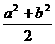 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不允分也不必要条件
[考点分析]本题考查平方不等式和充要条件,基础题。
解析:由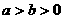 能推出
能推出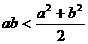 ;但反之不然,因此平方不等式的条件是
;但反之不然,因此平方不等式的条件是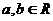 。
。
10.(上海卷)如果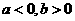 ,那么,下列不等式中正确的是( )
,那么,下列不等式中正确的是( )
(A)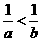 (B)
(B)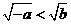 (C)
(C)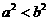 (D)
(D)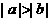
解:如果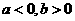 ,那么
,那么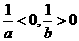 ,∴
,∴ 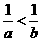 ,选A.
,选A.
9.(上海卷)若关于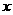 的不等式
的不等式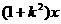 ≤
≤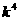 +4的解集是M,则对任意实常数
+4的解集是M,则对任意实常数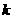 ,总有( )
,总有( )
(A)2∈M,0∈M; (B)2 M,0
M,0 M; (C)2∈M,0
M; (C)2∈M,0 M; (D)2
M; (D)2 M,0∈M.
M,0∈M.
解:选(A)
方法1:代入判断法,将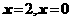 分别代入不等式中,判断关于
分别代入不等式中,判断关于 的不等式解集是否为
的不等式解集是否为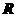 ;
;
方法2:求出不等式的解集: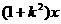 ≤
≤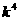 +4
+4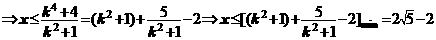 ;
;
8.(陕西卷)设x,y为正数, 则(x+y)( + )的最小值为( )
A. 6 B.9 C.12 D.15
解析:x,y为正数,(x+y)(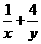 )≥
)≥ ≥9,选B.
≥9,选B.
7.(陕西卷)已知函数f(x)=ax2+2ax+4(a>0),若x1<x2 , x1+x2=0 , 则( )
A.f(x1)<f(x2) B.f(x1)=f(x2) C.f(x1)>f(x2) D.f(x1)与f(x2)的大小不能确定
解析:函数f(x)=ax2+2ax+4(a>0),二次函数的图象开口向上,对称轴为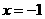 ,a>0,∴ x1+x2=0,x1与x2的中点为0,x1<x2,∴ x2到对称轴的距离大于x1到对称轴的距离,∴ f(x1)<f(x2)
,选A.
,a>0,∴ x1+x2=0,x1与x2的中点为0,x1<x2,∴ x2到对称轴的距离大于x1到对称轴的距离,∴ f(x1)<f(x2)
,选A.
6.(陕西卷)已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2,x1+x2=1-a,则( )
A.f(x1)<f(x2) B.f(x1)=f(x2) C.f(x1)>f(x2) D.f(x1)与f(x2)的大小不能确定
解析:函数f(x)=ax2+2ax+4(0<a<3),二次函数的图象开口向上,对称轴为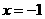 ,0<a<3,∴ x1+x2=1-a∈(-2,1),x1与x2的中点在(-1,
,0<a<3,∴ x1+x2=1-a∈(-2,1),x1与x2的中点在(-1,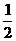 )之间,x1<x2,∴ x2到对称轴的距离大于x1到对称轴的距离,∴ f(x1)<f(x2)
,选A.
)之间,x1<x2,∴ x2到对称轴的距离大于x1到对称轴的距离,∴ f(x1)<f(x2)
,选A.
5.(陕西卷)已知不等式(x+y)( + )≥9对任意正实数x,y恒成立,则正实数a的最小值为( )
A.2 B.4 C.6 D.8
解析:不等式(x+y)(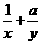 )≥9对任意正实数x,y恒成立,则
)≥9对任意正实数x,y恒成立,则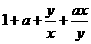 ≥
≥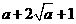 ≥9,∴
≥9,∴  ≥2或
≥2或 ≤-4(舍去),所以正实数a的最小值为4,选B.
≤-4(舍去),所以正实数a的最小值为4,选B.
4.(山东卷)设f(x)= 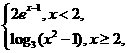
 则不等式f(x)>2的解集为
则不等式f(x)>2的解集为
(A)(1,2) (3,+∞)
(B)(
(3,+∞)
(B)(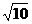 ,+∞)
,+∞)
(C)(1,2) (
(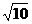 ,+∞)
(D)(1,2)
,+∞)
(D)(1,2)
解:令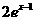 >2(x<2),解得1<x<2。令
>2(x<2),解得1<x<2。令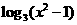 >2(x³2)解得xÎ(
>2(x³2)解得xÎ(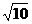 ,+∞)选C
,+∞)选C
3.(江西卷)若a>0,b>0,则不等式-b<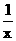 <a等价于( )
<a等价于( )
A.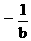 <x<0或0<x<
<x<0或0<x<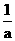 B.-
B.-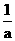 <x<
<x<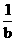 C.x<-
C.x<-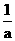 或x>
或x>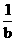 D.x<
D.x<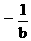 或x>
或x>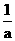
解: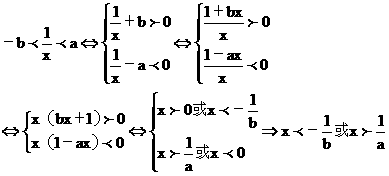
故选D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com