
题目列表(包括答案和解析)
31.(天津卷)设直线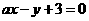 与圆
与圆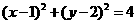 相交于
相交于 、
、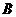 两点,且弦
两点,且弦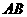 的长为
的长为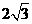 ,则
,则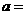 ____________.
____________.
解析:设直线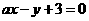 与圆
与圆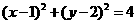 相交于
相交于 、
、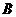 两点,且弦
两点,且弦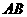 的长为
的长为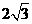 ,则圆心(1,2)到直线的距离等于1,
,则圆心(1,2)到直线的距离等于1,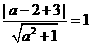 ,
,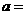 0.
0.
30.(四川卷)设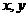 满足约束条件:
满足约束条件: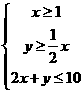 ,则
,则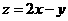 的最小值为
;
的最小值为
;
解析:设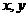 满足约束条件:
满足约束条件: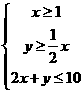 ,在直角坐标系中画出可行域△ABC,其中A(1,
,在直角坐标系中画出可行域△ABC,其中A(1,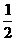 ),B(1,8),C(4,2),所以
),B(1,8),C(4,2),所以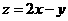 的最小值
的最小值 为-6。
为-6。
29.(上海卷)已知实数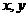 满足
满足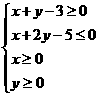 ,则
,则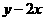 的最大值是_________.
的最大值是_________.
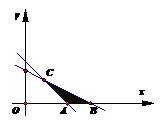 解析:实数
解析:实数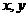 满足
满足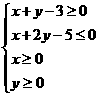 ,在坐标系中画出可行域,得三个交点为A(3,0)、B(5,0)、C(1,2),则
,在坐标系中画出可行域,得三个交点为A(3,0)、B(5,0)、C(1,2),则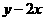 的最大值是0.
的最大值是0.
28.(上海卷)已知两条直线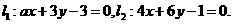 若
若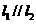 ,则
,则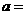 ____.
____.
解:两条直线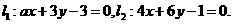 若
若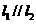 ,
,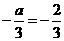 ,则
,则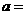 2.
2.
27.(上海卷)已知圆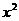 -4
-4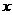 -4+
-4+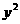 =0的圆心是点P,则点P到直线
=0的圆心是点P,则点P到直线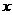 -
-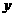 -1=0的距离是 .
-1=0的距离是 .
解:由已知得圆心为: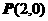 ,由点到直线距离公式得:
,由点到直线距离公式得: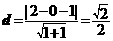 ;
;
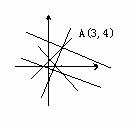
26.(全国II)过点(1,)的直线l将圆(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k= .
解析(数形结合)由图形可知点A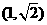 在圆
在圆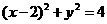 的内部, 圆心为O(2,0)要使得劣弧所对的圆心角最小,只能是直线
的内部, 圆心为O(2,0)要使得劣弧所对的圆心角最小,只能是直线 ,所以
,所以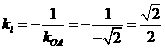
25.(全国卷I)设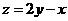 ,式中变量
,式中变量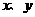 满足下列条件
满足下列条件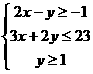 ,则z的最大值为_____________。
,则z的最大值为_____________。
解析:在坐标系中画出图象,三条线的交点分别是A(0,1),B(7,1),C(3,7),在△ABC中满足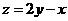 的最大值是点C,代入得最大值等于11.
的最大值是点C,代入得最大值等于11.
24.(江西卷)已知圆M:(x+cosq)2+(y-sinq)2=1,直线l:y=kx,下面四个命题:
(A) 对任意实数k与q,直线l和圆M相切;
(B) 对任意实数k与q,直线l和圆M有公共点;
(C) 对任意实数q,必存在实数k,使得直线l与和圆M相切
(D)对任意实数k,必存在实数q,使得直线l与和圆M相切
其中真命题的代号是______________(写出所有真命题的代号)
解:选(B)(D)圆心坐标为(-cosq,sinq),d=
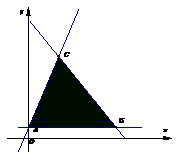
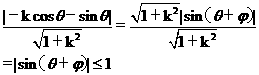
23.(江苏卷)设变量x、y满足约束条件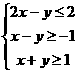 ,则
,则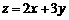
的最大值为
[正确解答] 画出可行域,得在直线2x-y=2与直线x-y=-1的交点
A(3,4)处,目标函数z最大值为18
22.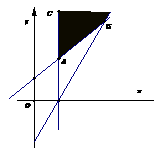 (湖南卷)已知
(湖南卷)已知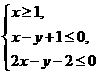 则
则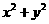 的最小值是
.
的最小值是
.
 解析:由
解析:由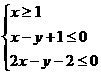 ,画出可行域,得交点A(1,2),B(3,4),则
,画出可行域,得交点A(1,2),B(3,4),则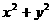 的最小值是5.
的最小值是5.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com