
题目列表(包括答案和解析)
25.(福建卷)每次抛掷一枚骰子(六个面上分别标以数字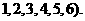
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
本小题主要考查概率的基本知识,运用数学知识解决实际问题的能力。满分12分。
解:(I)设A表示事件“抛掷2次,向上的数不同”,则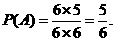
答:抛掷2次,向上的数不同的概率为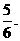
(II)设B表示事件“抛掷2次,向上的数之和为6”。
 向上的数之和为6的结果有
向上的数之和为6的结果有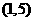 、
、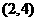 、
、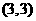 、
、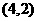 、
、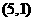 5种,
5种,
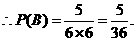
答:抛掷2次,向上的数之和为6的概率为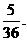
24.(北京卷)某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,
则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(Ⅰ) 应聘者用方案一考试通过的概率
p1=P(A·B·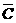 )+P(
)+P( ·B·C)+P(A·
·B·C)+P(A·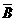 ·C)+P(A·B·C)
·C)+P(A·B·C)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9
=0.03+0.27+0.18+0.27=0.75.
(Ⅱ) 应聘者用方案二考试通过的概率
p2=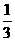 P(A·B)+
P(A·B)+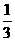 P(B·C)+
P(B·C)+ 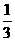 P(A·C)
P(A·C)
=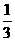 ×(0.5×0.6+0.6×0.9+0.5×0.9)=
×(0.5×0.6+0.6×0.9+0.5×0.9)=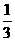 ×1.29=0.43
×1.29=0.43
23.(北京卷)某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是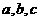 ,且三门课程考试是否及格相互之间没有影响.
,且三门课程考试是否及格相互之间没有影响.
(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率;
(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小.(说明理由)
解:设三门考试课程考试通过的事件分别为A,B,C,相应的概率为a,b,c
(1)考试三门课程,至少有两门及格的事件可表示为AB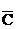 +A
+A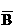 C+
C+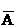 BC+ABC,设其概率为P1,则P1=ab(1-c)+a(1-b)c+(1-a)bc+abc=ab+ac+bc-2abc
BC+ABC,设其概率为P1,则P1=ab(1-c)+a(1-b)c+(1-a)bc+abc=ab+ac+bc-2abc
设在三门课程中,随机选取两门,这两门都及格的概率为P2,则P2=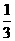 ab+
ab+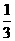 ac+
ac+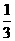 bc
bc
(2)P1-P2=(ab+ac+bc-2abc)-(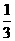 ab+
ab+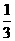 ac+
ac+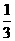 bc)=
bc)=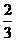 ab+
ab+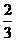 ac+
ac+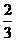 bc-2abc
bc-2abc
=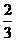 (ab+ac+bc-3abc)=
(ab+ac+bc-3abc)=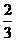 (ab(1-c)+ac(1-b)+bc(1-a))>0
(ab(1-c)+ac(1-b)+bc(1-a))>0
\P1>P2即用方案一的概率大于用方案二的概率.
22.(安徽卷)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。
(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率;
解:设“所选用的两种不同的添加剂的芳香度之和等于4”的事件为A,“所选用的两种不同的添加剂的芳香度之和不小于3”的事件为B
(Ⅰ)芳香度之和等于4的取法有2种: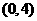 、
、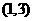 ,故
,故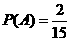 。
。
(Ⅱ)芳香度之和等于1的取法有1种: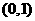 ;芳香度之和等于2的取法有1种:
;芳香度之和等于2的取法有1种: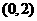 ,故
,故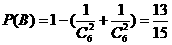 。
。
21.(安徽卷)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。
(Ⅰ)写出 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)
(Ⅱ)求 的数学期望
的数学期望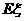 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)
解:(Ⅰ)
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
P |
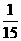 |
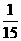 |
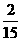 |
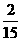 |
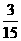 |
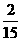 |
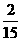 |
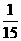 |
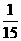 |
(Ⅱ)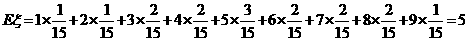
20.(上海春)同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语言描述为:若有限数列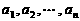 满足
满足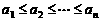 ,则
,则
(结论用数学式子表示).
解:如果在有限数列 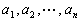 中,按顺序去掉一些高分
中,按顺序去掉一些高分 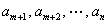 ,那么有不等关系
,那么有不等关系 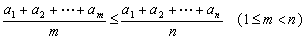 ; 如果在有限数列
; 如果在有限数列 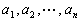 中,按顺序去掉一些低分
中,按顺序去掉一些低分 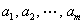 ,那么有不等关系
,那么有不等关系 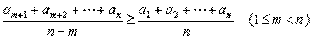 .从而应填
.从而应填
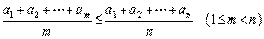 ,与
,与 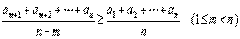 .
三、解答题(共27题)
.
三、解答题(共27题)
19.(四川卷)设离散型随机变量 可能取的值为1,2,3,4。
可能取的值为1,2,3,4。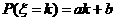 (
(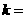 1,2,3,4)。又
1,2,3,4)。又 的数学期望
的数学期望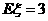 ,则
,则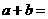 ;
;
解:设离散性随机变量 可能取的值为
可能取的值为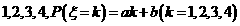 ,所以
,所以
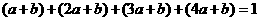 ,即
,即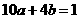 ,又
,又 的数学期望
的数学期望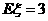 ,则
,则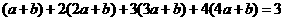 ,即
,即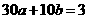 ,
,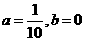 ,∴
,∴ 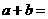
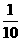 .
.
18.(上海卷)在一个小组中有8名女同学和4名男同学,从中任意地挑选2名同学担任交通安全宣传志愿者,那么选到的两名都是女同学的概率是______(结果用分数表示)。
解:在一个小组中有8名女同学和4名男同学,从中任意地挑选2名同学担任交通安全宣传志愿者,那么选到的两名都是女同学的概率是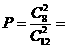
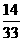 .
.
17.(上海卷)两部不同的长篇小说各由第一、二、三、四卷组成,每卷1本,共8本.将它们任意地排成一排,左边4本恰好都属于同一部小说的概率是 (结果用分数表示).
解:分为二步完成: 1) 两套中任取一套,再作全排列,有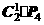 种方法;2) 剩下的一套全排列,有
种方法;2) 剩下的一套全排列,有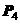 种方法;所以,所求概率为:
种方法;所以,所求概率为: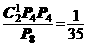 ;
;
16.(山东卷)某学校共有师生2400人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是 .
解:抽取教师为160-150=10人,所以学校教师人数为2400×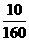 =150 人。
=150 人。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com