
题目列表(包括答案和解析)
45.(浙江卷)甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球.两甲,乙两袋中各任取2个球.
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为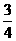 ,求n.
,求n.
本题主要考察排列组合、概率等基本知识,同时考察逻辑思维能力和数学应用能力。
解:(I)记“取到的4个球全是红球”为事件 .
.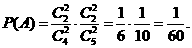
(II)记“取到的4个球至多有1个红球”为事件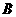 ,“取到的4个球只有1个红球”为事件
,“取到的4个球只有1个红球”为事件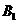 ,“取到的4个球全是白球”为事件
,“取到的4个球全是白球”为事件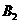 .由题意,得
.由题意,得
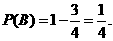
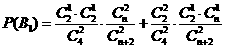
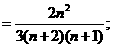

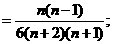
所以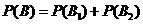
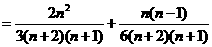
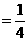 ,
,
化简,得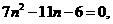
解得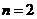 ,或
,或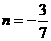 (舍去),
(舍去),
故 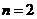 .
.
44.(天津卷)甲、乙两台机床相互没有影响地生产某种产品,甲机床产品的正品率是0.9,乙机床产品的正品率是0.95.
(Ⅰ)从甲机床生产的产品中任取3件,求其中恰有2件正品的概率(用数字作答);
(Ⅱ)从甲、乙两台机床生产的产品中各任取1件,求其中至少有1件正品的概率(用数字作答).
本小题考查互斥事件、相互独立事件的概率等基础知识,及分析和解决实际问题的能力。 解:(I)任取甲机床的3件产品恰有2件正品的概率为
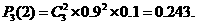
(II)解法一:记“任取甲机床的1件产品是正品”为事件A,“任取乙机床的1件产品是正品”为事件B。则任取甲、乙两台机床的产品各1件,其中至少有1件正品的概率为
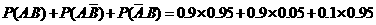
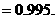
解法二:运用对立事件的概率公式,所求的概率为
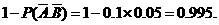
43.(天津卷)某射手进行射击训练,假设每次射击击中目标的概率为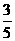 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);
(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);
(3)设随机变量 表示射手第3次击中目标时已射击的次数,求
表示射手第3次击中目标时已射击的次数,求 的分布列.
的分布列.
本小题考查互斥事件、相互独立事件的概率、离散型随机变量的分布列等基础知识,及分析和解决实际问题的能力.满分12分
解:(Ⅰ)记“射手射击1次,击中目标”为事件 ,则在3次射击中至少有两次连续击中目标的概率
,则在3次射击中至少有两次连续击中目标的概率
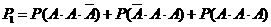
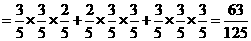
(Ⅱ)射手第3次击中目标时,恰好射击了4次的概率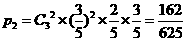
(Ⅲ)由题设,“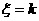 ”的概率为
”的概率为
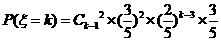
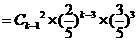 (
(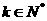 且
且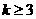 )
)
所以, 的分布列为:
的分布列为:
 |
3 |
4 |
… |
k |
… |
|
P |
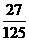 |
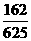 |
… |
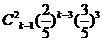 |
… |
42.(四川卷)某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”则该课程考核“合格”,甲、乙、丙三人在理论考核中合格的概率分别为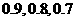 ;在实验考核中合格的概率分别为
;在实验考核中合格的概率分别为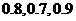 ,所有考核是否合格相互之间没有影响
,所有考核是否合格相互之间没有影响
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率。(结果保留三位小数)
本小题主要考察相互独立事件、互斥事件、对立事件等概率的计算方法,考察应用概率知识解决实际问题的能力。
解:记“甲理论考核合格”为事件 ;“乙理论考核合格”为事件
;“乙理论考核合格”为事件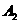 ;“丙理论考核合格”为事件
;“丙理论考核合格”为事件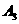 ;记
;记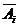 为
为 的对立事件,
的对立事件,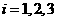 ;记“甲实验考核合格”为事件
;记“甲实验考核合格”为事件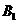 ;“乙实验考核合格”为事件
;“乙实验考核合格”为事件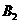 ;“丙实验考核合格”为事件
;“丙实验考核合格”为事件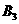 ;
;
(Ⅰ)记“理论考核中至少有两人合格”为事件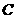 ,记
,记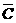 为
为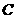 的对立事件
的对立事件
解法1: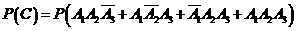
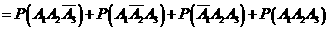
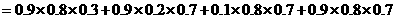
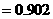
解法2: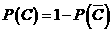
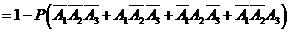
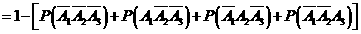
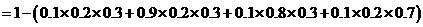
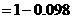
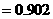
所以,理论考核中至少有两人合格的概率为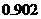
(Ⅱ)记“三人该课程考核都合格” 为事件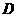
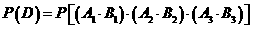
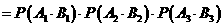
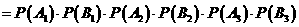
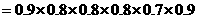
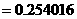
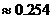
所以,这三人该课程考核都合格的概率为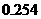
41.(陕西卷)甲、乙、丙3人投篮,投进的概率分别是, , .现3人各投篮1次,求:
(Ⅰ)3人都投进的概率;
(Ⅱ)3人中恰有2人投进的概率.
解: (Ⅰ)记"甲投进"为事件A1 , "乙投进"为事件A2 , "丙投进"为事件A3,
则 P(A1)= , P(A2)= , P(A3)= ,
∴ P(A1A2A3)=P(A1) ·P(A2) ·P(A3) = × ×=
∴3人都投进的概率为
(Ⅱ) 设“3人中恰有2人投进"为事件B
P(B)=P(A2A3)+P(A1A3)+P(A1A2)
=P()·P(A2)·P(A3)+P(A1)·P()·P(A3)+P(A1)·P(A2)·P()
=(1-)× × + ×(1-)× + × ×(1-) =
∴3人中恰有2人投进的概率为
40.(陕西卷)甲、乙、丙3人投篮,投进的概率分别是, , .
(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;
(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ.
解: (Ⅰ)记"甲投篮1次投进"为事件A1 , "乙投篮1次投进"为事件A2 , "丙投篮1次投进"为事件A3, "3人都没有投进"为事件A . 则 P(A1)= , P(A2)= , P(A3)= ,
∴ P(A) = P( .
.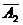 .
. )=P(
)=P( )·P(
)·P(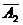 )·P(
)·P( )
)
= [1-P(A1)] ·[1-P (A2)] ·[1-P (A3)]=(1-)(1-)(1-)=
∴3人都没有投进的概率为 .
(Ⅱ)解法一: 随机变量ξ的可能值有0,1,2,3), ξ~ B(3, ),
P(ξ=k)=C3k()k()3-k (k=0,1,2,3) , Eξ=np = 3× = .
解法二: ξ的概率分布为:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
Eξ=0×+1×+2×+3×= .
39.(山东卷)盒中装着标有数字1,2,3,4的卡片各2张,从盒中任意任取3张,每张卡片被抽出的可能性都相等,求:
(Ⅰ)抽出的3张卡片上最大的数字是4的概率;
(Ⅱ)抽出的3张中有2张卡片上的数字是3的概念;
(Ⅲ)抽出的3张卡片上的数字互不相同的概率.
解:(I)“抽出的3张卡片上最大的数字是4”的事件记为A,由题意
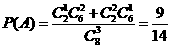
(II)“抽出的3张中有2张卡片上的数字是3”的事件记为B,则
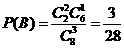
(III)“抽出的3张卡片上的数字互不相同”的事件记为C,“抽出的3张卡片上有两个数字相同”的事件记为D,由题意,C与D是对立事件,因为 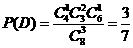
所以 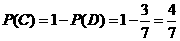 .
.
38.(山东卷)袋中装着标有数学1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用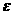 表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量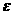 的概率分布和数学期望;
的概率分布和数学期望;
(3)计分介于20分到40分之间的概率.
解:(I)解法一:“一次取出的3个小球上的数字互不相同”的事件记为 ,
,
则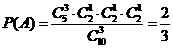
解法二:“一次取出的3个小球上的数字互不相同的事件记为A”,“一次取出的3个小球上有两个数字相同”的事件记为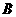 ,则事件
,则事件 和事件
和事件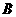 是互斥事件,因为
是互斥事件,因为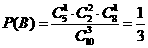 ,所以
,所以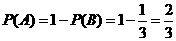 .
.
(II)由题意 有可能的取值为:2,3,4,5.
有可能的取值为:2,3,4,5.
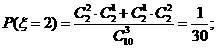
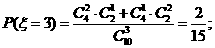
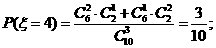
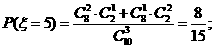
所以随机变量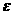 的概率分布为
的概率分布为
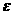 |
2 |
3 |
4 |
5 |
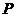 |
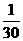 |
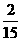 |
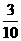 |
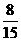 |
因此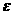 的数学期望为
的数学期望为
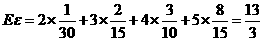
(Ⅲ)“一次取球所得计分介于20分到40分之间”的事件记为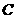 ,则
,则

37.(全国II)某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,再从每箱中任意出取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品。
(I)求取6件产品中有1件产品是二等品的概率。
(II)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝的概率。
解:设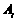 表示事件“第二箱中取出i件二等品”,i=0,1;
表示事件“第二箱中取出i件二等品”,i=0,1;
 表示事件“第三箱中取出i件二等品”,i=0,1,2;
表示事件“第三箱中取出i件二等品”,i=0,1,2;
(1)依题意所求的概率为
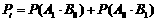
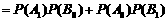
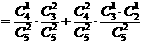
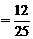
(2)解法一:所求的概率为
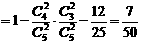
解法二:所求的概率为
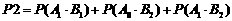
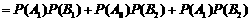
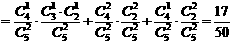
36.(全国II)某批产品成箱包装,每箱5件.一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品.
(Ⅰ)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(Ⅱ)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品级用户拒绝的概率.
解(1.) 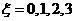
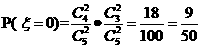
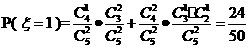
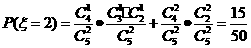
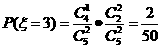
所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
|
P |
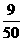 |
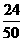 |
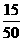 |
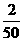 |
 的数学期望E(
的数学期望E( )=
)=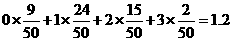
(2)P(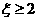 )=
)=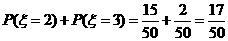
本题主要考察分布列的求法以及利用分布列求期望和概率,难度对于民族地区学生较大
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com