
题目列表(包括答案和解析)
8.(江西卷)在(x-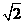 )2006 的二项展开式中,含x的奇次幂的项之和为S,当x=
)2006 的二项展开式中,含x的奇次幂的项之和为S,当x=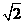 时,S等于( )
时,S等于( )
A.23008 B.-23008 C.23009 D.-23009
解:设(x-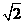 )2006=a0x2006+a1x2005+…+a2005x+a2006
)2006=a0x2006+a1x2005+…+a2005x+a2006
则当x=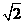 时,有a0(
时,有a0(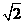 )2006+a1(
)2006+a1(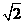 )2005+…+a2005(
)2005+…+a2005(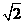 )+a2006=0 (1)
)+a2006=0 (1)
当x=-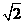 时,有a0(
时,有a0(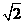 )2006-a1(
)2006-a1(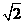 )2005+…-a2005(
)2005+…-a2005(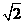 )+a2006=23009 (2)
)+a2006=23009 (2)
7.(江苏卷)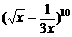 的展开式中含x的正整数指数幂的项数是
的展开式中含x的正整数指数幂的项数是
(A)0 (B)2 (C)4 (D)6
[思路点拨]本题主要考查二项式展开通项公式的有关知识.
[正确解答]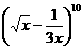 的展开式通项为
的展开式通项为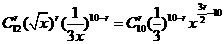 ,因此含x的正整数次幂的项共有2项.选B
,因此含x的正整数次幂的项共有2项.选B
[解后反思]多项式乘法的进位规则.在求系数过程中,尽量先化简,降底数的运算级别,尽量化成加减运算,在运算过程可以适当注意令值法的运用,例如求常数项,可令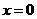 .在二项式的展开式中,要注意项的系数和二项式系数的区别.
.在二项式的展开式中,要注意项的系数和二项式系数的区别.
6.(湖南卷)在数字1,2,3与符号+,-五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是
A.6 B. 12 C. 18 D. 24
解析:先排列1,2,3,有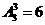 种排法,再将“+”,“-”两个符号插入,有
种排法,再将“+”,“-”两个符号插入,有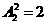 种方法,共有12种方法,选B.
种方法,共有12种方法,选B.
5.(湖南卷)若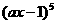 的展开式中
的展开式中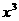 的系数是80,则实数a的值是
的系数是80,则实数a的值是
A.-2 B. 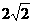 C.
C. 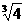 D. 2
D. 2
解析: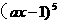 的展开式中
的展开式中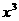 的系数
的系数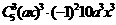 =
=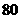 x3, 则实数
x3, 则实数 的值是2,选D
的值是2,选D
4.(湖南卷)某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有 ( )
A.16种 B.36种 C.42种 D.60种
解析:有两种情况,一是在两个城市分别投资1个项目、2个项目,此时有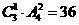 种方案,二是在三个城市各投资1个项目,有
种方案,二是在三个城市各投资1个项目,有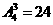 种方案,共计有60种方案,选D.
种方案,共计有60种方案,选D.
3.(湖北卷)在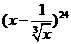 的展开式中,
的展开式中,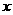 的幂的指数是整数的项共有
的幂的指数是整数的项共有
A.3项 B.4项 C.5项 D.6项
解: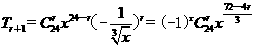 ,当r=0,3,6,9,12,15,18,21,24时,x的指数分别是24,20,16,12,8,4,0,-4,-8,其中16,8,4,0,-8均为2的整数次幂,故选C
,当r=0,3,6,9,12,15,18,21,24时,x的指数分别是24,20,16,12,8,4,0,-4,-8,其中16,8,4,0,-8均为2的整数次幂,故选C
2.(福建卷)从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中至少有1名女生,则选派方案共有
(A)108种 (B)186种 (C)216种 (D)270种
解析:从全部方案中减去只选派男生的方案数,合理的选派方案共有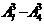 =186种,选B.
=186种,选B.
1.(北京卷)在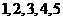 这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有
这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有
(A)36个 (B)24个 (C)18个 (D)6个
解:依题意,所选的三位数字有两种情况:(1)3个数字都是奇数,有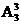 种方法(2)3个数字中有一个是奇数,有
种方法(2)3个数字中有一个是奇数,有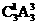 ,故共有
,故共有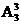 +
+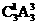 =24种方法,故选B
=24种方法,故选B
47.(重庆卷)甲、乙、丙三人在同一办公室工作。办公室只有一部电话机,设经过该机打进的电话是打给甲、乙、丙的概率依次为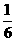 、
、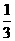 、
、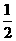 。若在一段时间内打进三个电话,且各个电话相互独立。求:
。若在一段时间内打进三个电话,且各个电话相互独立。求:
(Ⅰ)这三个电话是打给同一个人的概率;
(Ⅱ)这三个电话中恰有两个是打给甲的概率;
解:(Ⅰ)由互斥事件有一个发生的概率公式和独立事件同时发生的概率公式,
所求概率为: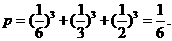
(Ⅱ)这是n=3,p=
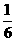 的独立重复试验,故所求概率为:
的独立重复试验,故所求概率为:
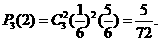
46.(重庆卷)某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有 5位乘客,且每位乘客在这三层的每一层下电梯的概率均为
5位乘客,且每位乘客在这三层的每一层下电梯的概率均为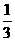 ,用ξ表示这5位乘客在第20层下电梯的人数.求:
,用ξ表示这5位乘客在第20层下电梯的人数.求:
(Ⅰ)随机变量ξ的分布列;
(Ⅱ)随机变量ξ的期望.
解:(1) 的所有可能值为0,1,2,3,4,5。由等可能性事件的概率公式得
的所有可能值为0,1,2,3,4,5。由等可能性事件的概率公式得
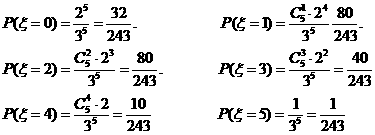
从而, 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
4 |
5 |
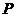 |
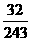 |
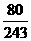 |
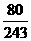 |
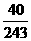 |
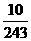 |
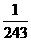 |
(II)由(I)得 的期望为
的期望为
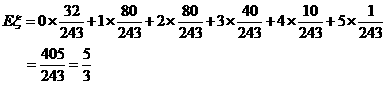
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com