
题目列表(包括答案和解析)
11.(辽宁卷)已知函数 ,则
,则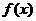 的值域是
的值域是
(A)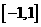 (B)
(B)  (C)
(C) 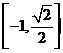 (D)
(D) 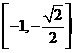
[解析]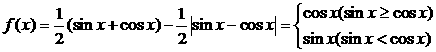
即等价于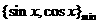 ,故选择答案C。
,故选择答案C。
[点评]本题考查绝对值的定义、分段函数、三角函数等知识,同时考查了简单的转化和估算能力。
10.(江西卷)函数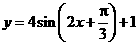 的最小正周期为( )
的最小正周期为( )
A.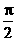 B.
B.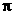 C.
C.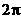 D.
D.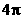
解:T=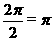 ,故选B
,故选B
8.(江苏卷)已知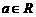 ,函数
,函数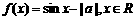 为奇函数,则a=
为奇函数,则a=
(A)0 (B)1 (C)-1 (D)±1
[思路点拨]本题考查函数的奇偶性,三角函数sinx的奇偶性的判断,本题是一道送分的概念题
[正确解答]解法1由题意可知, 得a=0
得a=0
解法2:函数的定义域为R,又f (x)为奇函数,故其图象必过原点即f (0)=0,所以得a=0,
解法3由f (x)是奇函数图象法函数画出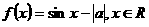 的图象选A
的图象选A
[解后反思]对数学概念及定理公式的深刻理解是解数学问题的关健,讨论函数的奇偶性,其前提条件是函数的定义域必须关于原点对称.
若函数f(x)为奇函数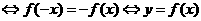 的图象关于原点对称.
的图象关于原点对称.
若函数f(x)为偶函数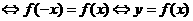 的图象关于y轴对称.
的图象关于y轴对称.
9(江苏卷)为了得到函数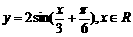 的图像,只需把函数
的图像,只需把函数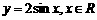 的图像上所有的点
的图像上所有的点
(A)向左平移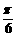 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的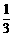 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移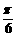 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的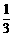 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移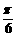 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移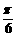 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
[思路点拨]本题主要考三角函数的图象变换,这是一道平时训练的比较多的一种类型。
[正确解答]先将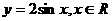 的图象向左平移
的图象向左平移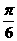 个单位长度,
个单位长度,
得到函数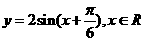 的图象,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数
的图象,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数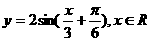 的图像,选择C。
的图像,选择C。
[解后反思]由函数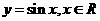 的图象经过变换得到函数
的图象经过变换得到函数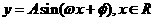
(1).y=Asinx,xÎR(A>0且A¹1)的图象可以看作把正弦曲线上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍得到的
(2)函数y=sinωx, xÎR (ω>0且ω¹1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的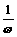 倍(纵坐标不变)
倍(纵坐标不变)
(3)函数y=sin(x+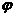 ),x∈R(其中
),x∈R(其中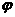 ≠0)的图象,可以看作把正弦曲线上所有点向左(当
≠0)的图象,可以看作把正弦曲线上所有点向左(当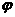 >0时)或向右(当
>0时)或向右(当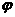 <0时=平行移动|
<0时=平行移动|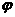 |个单位长度而得到
|个单位长度而得到 (用平移法注意讲清方向:“加左”“减右”),可以先平移变换后伸缩变换,也可以先伸缩变换后平移变换,但注意:先伸缩时,平移的单位把x前面的系数提取出来。
(用平移法注意讲清方向:“加左”“减右”),可以先平移变换后伸缩变换,也可以先伸缩变换后平移变换,但注意:先伸缩时,平移的单位把x前面的系数提取出来。
7.(湖南卷)设点P是函数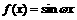 的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值
的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值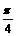 ,则
,则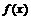 的最小正周期是
的最小正周期是
A.2π
B. π C. 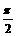 D.
D. 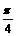
解析:设点P是函数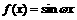 的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值
的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值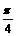 ,∴ 最小正周期为π,选B.
,∴ 最小正周期为π,选B.
6.(湖北卷)若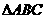 的内角
的内角 满足
满足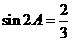 ,则
,则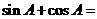
A.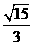 B.
B.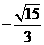 C.
C.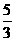 D.
D.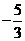
解:由sin2A=2sinAcosA>0,可知A这锐角,所以sinA+cosA>0,又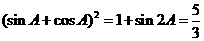 ,故选A
,故选A
5.(福建卷)已知函数f(x)=2sin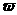 x(
x(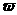 >0)在区间[
>0)在区间[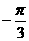 ,
,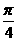 ]上的最小值是-2,则
]上的最小值是-2,则 的最小值等于
的最小值等于
A.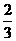 B.
B.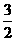 C.2
D.3
C.2
D.3
解:函数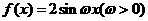 在区间
在区间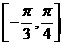 上的最小值是
上的最小值是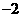 ,则ωx的取值范围是
,则ωx的取值范围是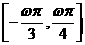 , ∴
, ∴ 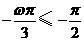 或
或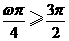 ,∴
,∴  的最小值等于
的最小值等于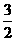 ,选B.
,选B.
4.(福建卷)已知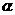 ∈(
∈(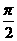 ,
,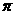 ),sin
),sin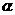 =
=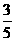 ,则tan(
,则tan(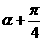 )等于
)等于
A.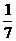 B.7
C.-
B.7
C.- 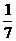 D.-7
D.-7
解:由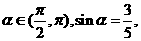 则
则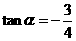 ,
,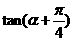 =
=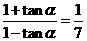 ,选A.
,选A.
3.(北京卷)函数y=1+cosx的图象
(A)关于x轴对称 (B)关于y轴对称
(C)关于原点对称 (D)关于直线x=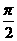 对称
对称
解:函数y=1+cos是偶函数,故选B
2.(安徽卷)设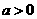 ,对于函数
,对于函数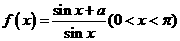 ,下列结论正确的是
,下列结论正确的是
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
解:令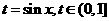 ,则函数
,则函数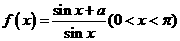 的值域为函数
的值域为函数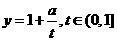 的值域,又
的值域,又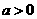 ,所以
,所以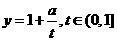 是一个减函减,故选B。
是一个减函减,故选B。
1.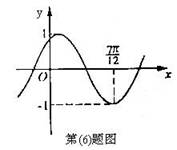 (安徽卷)将函数
(安徽卷)将函数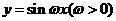 的图象按向量
的图象按向量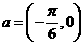 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
A.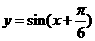 B.
B.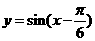
C.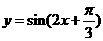 D.
D.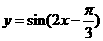
解:将函数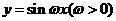 的图象按向量
的图象按向量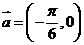 平移,平移后的图象所对应的解析式为
平移,平移后的图象所对应的解析式为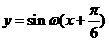 ,由图象知,
,由图象知,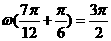 ,所以
,所以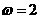 ,因此选C。
,因此选C。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com