
题目列表(包括答案和解析)
7.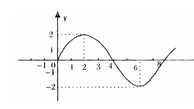 函数
函数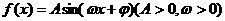 的部分图象如右图所示,则
的部分图象如右图所示,则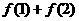
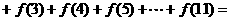 ( )
( )
A.2
B.2+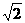
C.2+2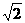 D.-2-2
D.-2-2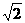
6.在直角坐标平面内,向量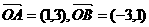 在直线l上的射影长相等,且直线l的倾斜角为锐角,则直线l的斜率为 ( )
在直线l上的射影长相等,且直线l的倾斜角为锐角,则直线l的斜率为 ( )
A.1 B.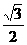 C.
C.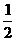 D.
D.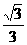
5.已知圆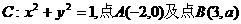 ,从A点观察B点,要使视线不被圆C挡住,则实数a的取值范围是( )
,从A点观察B点,要使视线不被圆C挡住,则实数a的取值范围是( )
A.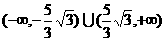 B.
B.
C.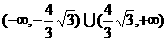 D.
D.
4.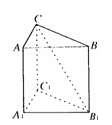 在正三棱柱ABC-A1B1C1中,若AB=AA1,则直线CB1与平面AA1B1B所成角的正弦值是 ( )
在正三棱柱ABC-A1B1C1中,若AB=AA1,则直线CB1与平面AA1B1B所成角的正弦值是 ( )
A.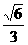 B.
B.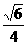 C.
C.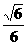 D.
D.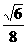
3.设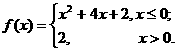 则关于x的方程
则关于x的方程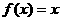 的解的个数为( )
的解的个数为( )
A.1 B.2 C.3 D.4
2.已知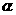 、
、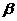 是两个不同的平面,直线
是两个不同的平面,直线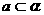 ,直线
,直线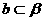 。命题
。命题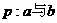 无公共点;命题
无公共点;命题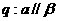 。则p是q的 ( )
。则p是q的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
1.设全集U={2,4,6,8,10},集合A={2,4,6},B={4,8},则A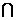 (
( UB)=( )
UB)=( )
A.{4} B.{6} C.{4,6} D.{2,6}
22.设函数f(x)的定义域为R,对于任意实数x,y,总有f(x+y)=f(x)f(y),且当x>0时,0<f(x)<1.
(1)求f(0)的值;(2)证明:当x<0时,f(x)>1;
(3)证明:f(x)在R上单调递减;(4)若M={y|f(y)·f(1-a)≥f(1)},N={y|f(ax2+x+1-y)=1,x∈R},且M∩N≠φ,求a的取值范围.
21.今有甲、乙两个篮球队进行比赛,规定两队中有一队胜4场则整个比赛宣告结束.假设甲、乙两队在每场比赛中获胜的概率都是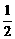 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ.
(Ⅰ)求ξ大于5的概率;
(Ⅱ)求ξ的分布列与数学期望.
20.有一块边长为4米的正方形钢板,现对其进行切割,焊接成一个长方体形无盖容器(切、焊损耗忽略不计),有人用数学知识作了如下设计:在钢板的四个角处各切去一个小正方形,剩余部分围成一个长方体,该长方体的高为小正方形边长.
(1)请你求出这种切割、焊接而成的长方体的最大容积v1;
(2)由于上述设计对材料有所浪费,请你重新设计,减少浪费,而且所得长方体容器的容积v2>v1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com