
题目列表(包括答案和解析)
16.设定义域为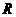 的函数
的函数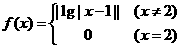 ,若
,若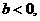 则关于
则关于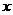 的方程
的方程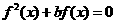 的不同实根有 ________个.
的不同实根有 ________个.
15.数列{an}满足递推式an=3an-1+3n-1(n≥2),又a1=5,则使得{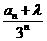 }为等差数列的实数λ=_____________
}为等差数列的实数λ=_____________
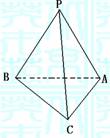
14.如图,在三棱锥P-ABC中,PA=PB=PC=BC,
且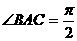 ,则PA与底面ABC所成角为
,则PA与底面ABC所成角为
.
13.
 设实数x, y满足
设实数x, y满足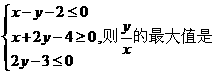 .
.
12.抛物线y=-x2上的点到直线4x+3y-8=0的距离的最小值是____.
11.不等式x+3>|2x-1|的解集为______________.
(17)已知函数f(x)=A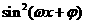 (A>0,
(A>0, >0,0<
>0,0<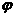 <
<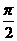 函数,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
函数,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求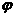 ;
;
(2)计算f(1)+f(2)+ f(3)… +f(2 007).
(18)A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止.求掷硬币的次数不大于7次时游戏终止的概率.
(19)(本小题满分12分)
如图,已知平面A1B1C1平行于三棱锥F-ABC的底面ABC,等边∆ AB1C所在的平面与底面ABC垂直,且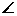 ACB=90°,设AC=2a,BC=a.
ACB=90°,设AC=2a,BC=a.
(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;
(2)求点A到平面FBC的距离;
(3)求二面角A-FB-C的大小.
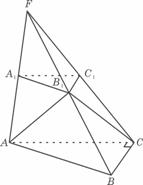
(19题图)
(20)双曲线C与椭圆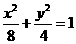 有相同的焦点,直线y=
有相同的焦点,直线y=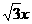 为C的一条渐近线.
为C的一条渐近线.
(1) 求双曲线C的方程;
(2) 过点P(0,4)的直线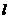 ,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当
,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当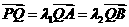 ,且
,且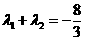 时,求Q点的坐标.
时,求Q点的坐标.
(21)已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中=1,2,3,…
(1) 证明数列{lg(1+an)}是等比数列;
(2) 设Tn=(1+a1) (1+a2) …(1+an),求Tn及数列{an}的通项;
(3) 记bn=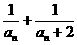 ,求{bn}数列的前项和Sn,并证明Sn+
,求{bn}数列的前项和Sn,并证明Sn+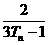 =1.
=1.
(11)不等式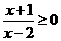 的解集是 .
的解集是 .
(12)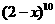 展开式中
展开式中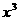 的系数为___________(用数字作答)。’
的系数为___________(用数字作答)。’
(13)双曲线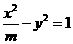 上的点到左焦点的距离与到左准线的距离的比是3,则
上的点到左焦点的距离与到左准线的距离的比是3,则 等于
等于
 (14)已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于
(14)已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于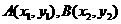 两点,则
两点,则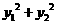 的最小值是
.
的最小值是
.
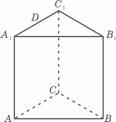
(15)如右图,已知正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的中点,则直线AD 与平面B1DC所成角的正弦值为 .
(16)下列四个命题中,真命题的序号有 (写出所有真命题的序号).
①将函数y=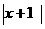 的图象按向量v=(-1,0)平移,得到的图象对应的函数表达式为y=
的图象按向量v=(-1,0)平移,得到的图象对应的函数表达式为y=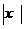
②圆x2+y2+4x+2y+1=0与直线y=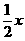 相交,所得弦长为2
相交,所得弦长为2
③若sin(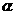 +
+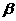 )=
)=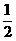 ,sin(
,sin(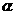 -
-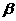 )=
)=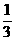 ,则tan
,则tan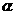 cot
cot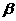 =5
=5
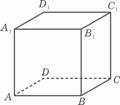 ④如右图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.
④如右图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.
(
(1)定义集合运算:A⊙B={z︳z= xy(x+y),x∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为
(A)0 (B)6 (C)12 (D)18
(2)函数y=1+ax(0<a<1)的反函数的图象大致是

(A) (B) (C) (D)
(3)设f(x)= 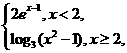
 则不等式f(x)>2的解集为
则不等式f(x)>2的解集为
(A)(1,2)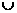 (3,+∞)
(B)(
(3,+∞)
(B)(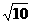 ,+∞)
,+∞)
(C)(1,2)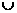 (
(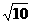 ,+∞) (D)(1,2)
,+∞) (D)(1,2)
(4)在△ABC中,角A、B、C的对边分别为a、b、c,A=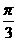 ,a=
,a=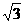 ,b=1,则c=
,b=1,则c=
(A) 1
(B)2
(C)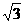 -1
(D)
-1
(D)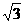
(5)设向量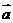 =(1, -2),
=(1, -2),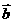 =(-2,4),
=(-2,4),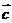 =(-1,-2),若表示向量4
=(-1,-2),若表示向量4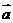 ,4
,4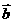 -2
-2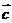 ,2(
,2(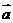 -
-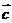 ),
),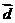 的有向线段首尾相接能构成四边形,则向量
的有向线段首尾相接能构成四边形,则向量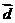 为
为
(A)(2,12) (B)(-2,12) (C)(2,-12) (D)(-2,-12)
(6)已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则,f(6)的值为
(A)-1 (B) 0 (C) 1 (D)2
(7)在给定椭圆中,过焦点且垂直于长轴的弦长为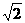 ,焦点到相应准线的距离为1,则该椭圆的离心率为
,焦点到相应准线的距离为1,则该椭圆的离心率为
(A)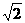 (B)
(B)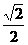 (C)
(C) 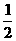 (D)
(D)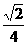
(8)设p:x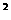 -x-20>0,q:
-x-20>0,q: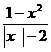 <0,则p是q的
<0,则p是q的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(9)已知集合A={5},B={1,2},C={1,3,4},从这三个集合中各取一个元素构成空间直角坐标系中点的坐标,则确定的不同点的个数为
(A)33 (B) 34 (C) 35 (D)36
(10)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为
 (A)
(A)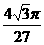 (B)
(B)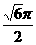 (C)
(C)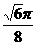 (D)
(D)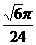
(10题图)
21.(本小题满分14分)平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,
-2),点C满足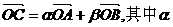 、
、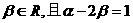
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线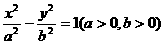 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: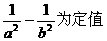 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com