
题目列表(包括答案和解析)
10.有以下四个命题:(1)2n>2n+1(n≥3) (2)2+4+6+…+2n=n2+n+2(n≥1) (3)凸n边形内角和为f(n)=(n-1)π(n≥3) (4)凸n边形对角线条数f(n)=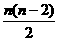 (n≥4).其中满足“假设n=k(k∈N,k≥n0).时命题成立,则当n=k+1时命题也成立.”但不满足“当n=n0(n0是题中给定的n的初始值)时命题成立”的命题序号是___________.
(n≥4).其中满足“假设n=k(k∈N,k≥n0).时命题成立,则当n=k+1时命题也成立.”但不满足“当n=n0(n0是题中给定的n的初始值)时命题成立”的命题序号是___________.
9.设f(n)=(1+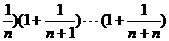 ,用数学归纳法证明f(n)≥3.在“假设n=k时成立”后,f(k+1)与f(k)的关系是f(k+1)=f(k)·___________.
,用数学归纳法证明f(n)≥3.在“假设n=k时成立”后,f(k+1)与f(k)的关系是f(k+1)=f(k)·___________.
8.观察下列式子:1+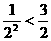 ,1+
,1+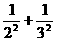 <
<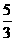 ,1+
,1+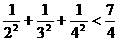 ,…则可归纳出:___________.
,…则可归纳出:___________.
7.凸n边形内角和为f(k),则凸k+1边形的内角和f(k+1)=f(k)+___________.
6.上一个n级台阶,若每步可上一级或两级,设上法总数为f(n),则下列猜想中正确的是
A.f(n)=n B.f(n)=f(n-1)+f(n-2)
C.f(n)=f(n-1)·f(n-2) D.f(n)=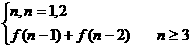
5.证明1+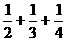 +…+
+…+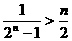 (n∈N*),假设n=k时成立,当n=k+1时,左端增加的项数是
(n∈N*),假设n=k时成立,当n=k+1时,左端增加的项数是
A. 1项 B.k-1项 C.k项 D.2k项
4.用数学归纳法证明(n+1)(n+2)…(n+n)=2n·1·3·5·…(2n-1)(n∈N*)时,假设n=k时成立,若证n=k+1时也成立,两边同乘
A.2k+1 B.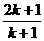 C.
C.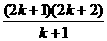 D.
D.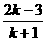
3.用数学归纳法证明不等式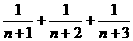 +…+
+…+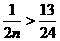 (n≥2,n∈N*)的过程中,由n=k逆推到n=k+1时的不等式左边
(n≥2,n∈N*)的过程中,由n=k逆推到n=k+1时的不等式左边
A. 增加了1项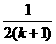 ; B.增加了“
; B.增加了“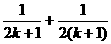 ”,又减少了“
”,又减少了“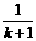 ”
”
C.增加了2项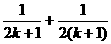 D.增加了
D.增加了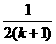 ,减少了
,减少了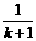
2.等式12+22+32+…+n2=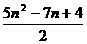
A.n为任何自然数时都成立;B.仅当n=1,2,3时成立
C.n=4时成立,n=5时不成立;D.仅当n=4时不成立
1.在应用数学归纳法证明凸n边形的对角线为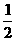 n(n-3)条时,第一步验证n等于
n(n-3)条时,第一步验证n等于
A. 1 B.2 C.3 D.0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com