
题目列表(包括答案和解析)
4.已知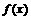 是R上的增函数,若令
是R上的增函数,若令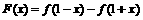 ,则
,则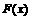 是R上的
是R上的
(A) 增函数 (B) 减函数
(C) 先减后增的函数 (D) 先增后减的函数
3.设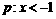 或
或 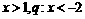 或
或 ,则
,则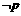 是
是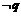 的
的
(A) 充分但不必要条件 (B) 必要但不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
2.若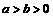 ,则下列不等式中总成立的是
,则下列不等式中总成立的是
(A)  (B)
(B)
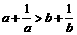
(C) 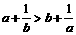 (D)
(D)
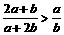
1.lg8+3lg5的值为
(A) -3 (B) -1 (C) 1 (D) 3
22.(共13分)
已知定义在(-1,1)上的函数f (x)满足 ,且对x,y
,且对x,y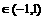 时,有
时,有
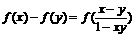 。
。
(I)判断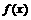 在(-1,1)上的奇偶性,并证明之;
在(-1,1)上的奇偶性,并证明之;
(II)令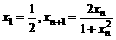 ,求数列
,求数列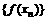 的通项公式;
的通项公式;
(III)设Tn为数列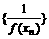 的前n项和,问是否存在正整数m,使得对任意的
的前n项和,问是否存在正整数m,使得对任意的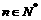 ,有
,有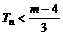 成立?若存在,求出m的最小值;若不存在,则说明理由。
成立?若存在,求出m的最小值;若不存在,则说明理由。
成都市2006届高中毕业班第一次诊断性检测题
21.(共12分)
某西部山区的某种特产由于运输的原因,长期只能在当地销售,当地政府对该项特产的销售投资收益为:每投入x万元,可获得利润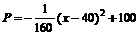 万元。当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入x万元,可获利润
万元。当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入x万元,可获利润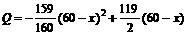 万元。问从10年的累积利润看,该规划方案是否可行?
万元。问从10年的累积利润看,该规划方案是否可行?
20.(共12分)
已知向量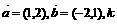 、t为正实数,
、t为正实数,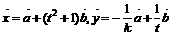 。
。
(I)若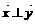 ,求k的最大值;
,求k的最大值;
(II)是否存在k、t使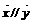 ?若存在,求出k的取值范围;若不存在,请说明理由。
?若存在,求出k的取值范围;若不存在,请说明理由。
19.(共14分)
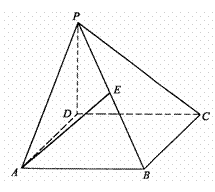 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点。
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点。
(I)求异面直线PD、AE所成的角;
(II)在平面PAD内求一点F,使得EF⊥平面PBC;
(III)求二面角F-PC-E的大小。
18.(共11分)
已知ΔABC中,角A、B、C所对边分别是a、b、c,b<a<c且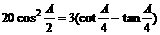 。求sin2A的值。
。求sin2A的值。
解答应写出文字说明、证明过程或推演步骤。
17.(共12分)
甲、乙两人参加一项智力测试。已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题。规定每位参赛者都从备选题中随机抽出3道题进行测试,至少答对2道题才算通过。
(I)求甲答对试题数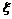 的概率分布及数学期望;
的概率分布及数学期望;
(II)求甲、乙两人至少有一人通过测试的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com