
题目列表(包括答案和解析)
6.
M(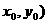 为圆
为圆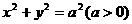 内异于圆心的一点,则直线
内异于圆心的一点,则直线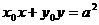 与该圆的位置关系为 ( )
与该圆的位置关系为 ( )
A.相切 B.相交 C.相离 D.相切或相交
5.
已知a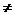 b,且a
b,且a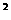 sin
sin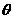 +acos
+acos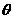 -
-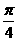 =0 ,b
=0 ,b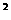 sin
sin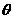 +bcos
+bcos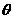 -
-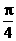 =0,则连接(a,a
=0,则连接(a,a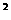 ),
),
(b,b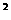 )两点的直线与单位圆的位置关系是
( )
)两点的直线与单位圆的位置关系是
( )
A.相交 B.相切 C.相离 D.不能确定
4.
定义在R上的函数y=f(x),在(-∞,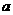 )上是增函数,且函数 y=f(x+
)上是增函数,且函数 y=f(x+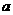 )是偶函数,当x1<
)是偶函数,当x1<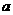 ,x2>
,x2>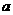 且
且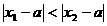 时,有
( )
时,有
( )
A.f(2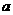 -x1)> f(2
-x1)> f(2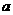 -x2) B.f(2
-x2) B.f(2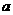 -x1)= f(2
-x1)= f(2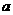 -x2)
-x2)
C.f(2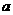 -x1)< f(2
-x1)< f(2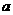 -x2) D.-f(2
-x2) D.-f(2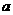 -x1)< f(x2-2
-x1)< f(x2-2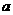 )
)
3. 对“a、b、c是不全相等的正数”,给出下列判断:
①(a-b)2+(b-c)2+(c-a)2≠0; ②a>b与a<b及a≠c中至少有一个成立;
③a≠c,b≠c,a≠b不能同时成立.
其中判断正确的个数为 ( )
A.0个 B.1个 C.2个 D.3个
2.
设实数x,
y满足x + y=4, 则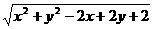 的最小值为 ( )
的最小值为 ( )
A. 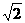 B.4 C.2
B.4 C.2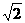 D.8
D.8
1.
已知实数a、b、c满足b+c=6-4a+3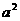 ,c-b=4-4a+
,c-b=4-4a+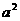 ,则a、b、c的大小关系是
( )
,则a、b、c的大小关系是
( )
A.c≥b>a B.a>c≥b C.c>b>a D.a>c>b
22. (文)如图甲、乙连接的6个元件,它们断电的概率第一个为P1=0.6,第二个为P2=0.2,其余四个都为P=0.3.分别求甲断电、乙通电的概率.

(理)已知a>1,数列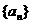 的通项公式是
的通项公式是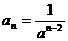 ,前n项和记作
,前n项和记作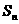 (n=1,2,…),规定
(n=1,2,…),规定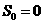 .函数
.函数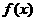 在
在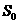 处和每个区间(
处和每个区间(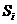 ,
,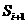 )(i=0,1,2,…)上有定义,且
)(i=0,1,2,…)上有定义,且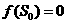 ,
,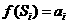 (i=1,2,…).当
(i=1,2,…).当 (
(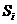 ,
,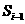 )时,f(x)的图像完全落在连结点
)时,f(x)的图像完全落在连结点 (
(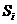 ,
,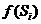 )与点
)与点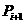 (
(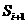 ,
,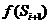 )的线段上.
)的线段上.
(Ⅰ)求f(x)的定义域;
(Ⅱ)设f(x)的图像与坐标轴及直线l: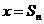 (n=1,2,…)围成的图形面积为
(n=1,2,…)围成的图形面积为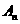 ,
,
求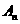 及
及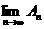 ;
;
(Ⅲ)若存在正整数n,使得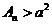 ,求a的取值范围.
,求a的取值范围.
21.
平面上两个质点A、B 分别位于(0,0),(2,2),在某一时刻同时开始,每隔1秒钟向上下左右任一方向移动1个单位,已知质点A向左右移动的概率都是 向上下移动的概率分别是
向上下移动的概率分别是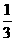 和
和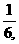 质点B向各个方向移动的概率是
质点B向各个方向移动的概率是
求:(1)4秒钟后A到达C(1,1)的概率;
(2)三秒钟后,A,B同时到达D(1,2)的概率
20. 已知10件产品中有3件是次品.
(1)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(2)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
19. 已知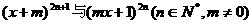 的展开式中含xn项的
的展开式中含xn项的
系数相等,求实数m的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com