
题目列表(包括答案和解析)
22.
如图所示:正四棱锥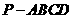 中,侧棱
中,侧棱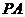 与底面
与底面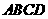 所成的角的正切值为
所成的角的正切值为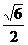 ,
,
(1)求侧面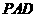 与底面
与底面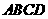 所成的二面角的大小;
所成的二面角的大小;
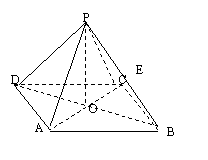 (2)若E是
(2)若E是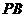 的中点,求异面直线PD与AE所成角的正切值;
的中点,求异面直线PD与AE所成角的正切值;
(3)在侧面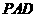 上寻找一点F,使EF⊥侧面
上寻找一点F,使EF⊥侧面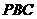 ,试确定点
,试确定点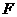 的位置,并加以证明.
的位置,并加以证明.
21. 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.点E在棱PA上,且PE=2EA.
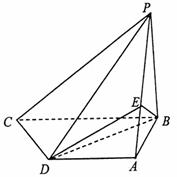 (1)求异面直线PA与CD所成的角;
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A-BE-D的大小.(用反三角函数表示).
20. 如图,直三棱柱ABC-A B
B C
C 中,AC=BC=AA
中,AC=BC=AA =2,
=2, 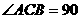
 ,E为BB
,E为BB 中
中
点,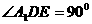 .
.
(1)求证:CD 面A
面A ABB
ABB ;
;
(2)求二面角C-A E-D的大小.
E-D的大小.
19.
已知在四面体ABCD中,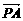 = a,
= a,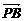 = b,
= b,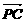 = c,G∈平面ABC.
= c,G∈平面ABC.
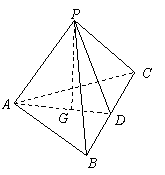 (1)若G为△ABC的重心,试证明
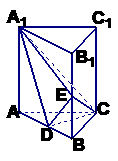
(1)若G为△ABC的重心,试证明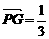 (a+b+c);
(a+b+c);
(2)试问(1)的逆命题是否成立?并证明你的结论.
18. 如图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.
(1)沿图中虚线将它们折叠起业,使P、Q、R、S四点重合,请画出其直观图,试问需要几个这样的几何体才能拼成一个棱长为6的正方体ABCD-A1B1C1D1?
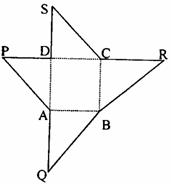 (2)设正方体ABCD-A1B1C1D1的棱CC1的中点为E,求平面AB1E与平面ABC所成二面角(锐角)的余弦值.
(2)设正方体ABCD-A1B1C1D1的棱CC1的中点为E,求平面AB1E与平面ABC所成二面角(锐角)的余弦值.
17.
已知定点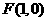 ,动点
,动点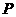 (异于原点)在
(异于原点)在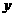 轴上运动,连接PF,过点
轴上运动,连接PF,过点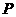 作
作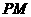 交
交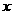 轴于点
轴于点 ,并延长
,并延长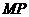 到点
到点 ,且
,且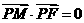 ,
,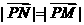 .
.
(1)求动点 的轨迹
的轨迹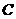 的方程;
的方程;
(2)若直线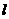 与动点
与动点 的轨迹交于
的轨迹交于 、
、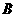 两点,若
两点,若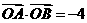 且
且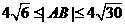 ,求直线
,求直线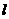 的斜率
的斜率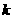 的取值范围.
的取值范围.
16. 在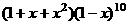 的展开式中,
的展开式中,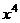 项的系数是
项的系数是
15. 某学校要从高三的6个班中派9名同学参加市中学生外语口语演讲,每班至少派1人,则这9个名额的分配方案共有 种.(用数字作答)
14. 一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为__________________.
13. 若椭圆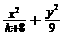 =1的离心率为
=1的离心率为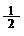 ,则k的值为 .
,则k的值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com