
题目列表(包括答案和解析)
20. (14分)己知函数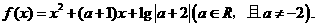
① 若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和,求g(x)和h(x)的解析式.
② 命题P:函数f(x)在区间 上是增函数;命题Q:函数g(x)是减函数.如果命题P、Q有且仅有一个是真命题,求
上是增函数;命题Q:函数g(x)是减函数.如果命题P、Q有且仅有一个是真命题,求 的取值范围.
的取值范围.
③ 在②的条件下,比较f(2)与3-lg2的大小.

21(14分)设点集 ,点
,点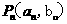 在
在
L中,p1 为L与y轴的交点,数列 的前n项和Sn=n2 .
的前n项和Sn=n2 .
⑴求数列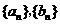 的通项公式.
的通项公式.
⑵若 ,计算
,计算
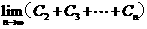 .
.
⑶ 设函数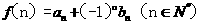 ,足否存在
,足否存在  ,使得f(k+10)=3f(k),
,使得f(k+10)=3f(k),
若存在,求出k的值;若不存在,说明理由.
望城县第一中学2006届高三第三次月考数学试卷
命题:陈国军 时量:120分钟 总分150分(第1卷)客观题(理)
18.( 12分)己知向量 =(
=( ),
),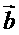 =(
=( ),
),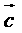 =(3,0).①若
=(3,0).①若 ,且
,且 都为锐角,求
都为锐角,求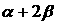 的值.
的值.
②若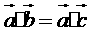 ,且
,且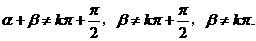 求
求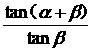 的值.
的值.
。
19,(14分)某工厂有容量为300吨的水塔一个,每天从早上6时起到晚上10时止供应该厂生活和生产用水。已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间 (单位:小时,定义早上6时
(单位:小时,定义早上6时 =0)的函数关系式为
=0)的函数关系式为 ,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级,每小时的进水量增加10吨,若某天水塔原有水100吨,在供水同时打开进水管。
,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级,每小时的进水量增加10吨,若某天水塔原有水100吨,在供水同时打开进水管。
(1)设进水量选用第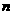 级,写出在
级,写出在 时刻水的存有量;
时刻水的存有量;
(2)问进水量选择第几级,既能保证该厂用水(水塔中水不空)又不会使水溢出。
(注:存有量=进水量-用水量+原有量,用水量=生活用水量+工业用水量。)
16、(14分)已知M(2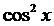 , 1), N (1,
, 1), N (1, 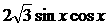 +a) (x,a∈R, a是常数),
+a) (x,a∈R, a是常数),
且 y = 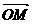

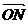 (O是坐标原点).
(O是坐标原点).
①求y关于x的函数关系式 y = f ( x ) ,
②若x∈[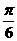 ,
, ]时,f ( x
) 的最小值为2,求a的值,并求f(x)的最小正周期.
]时,f ( x
) 的最小值为2,求a的值,并求f(x)的最小正周期.
③在②下说明f (x)( )的图像可由y=2sin2x(
)的图像可由y=2sin2x( )的图像经过怎样的变换而得到。
)的图像经过怎样的变换而得到。
11.____________, 12._____________, 13.____________;14____________,15.________________
22.(本题满分14分)已知函数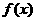 =
= (
(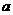 >0)
>0)
(Ⅰ)证明:函数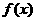 在区间(0,+∞)上是单调递增函数;
在区间(0,+∞)上是单调递增函数;
(Ⅱ)若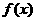 在
在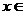 [m,n](其中m>0)的值域是[m,n],求a的取值范围;
[m,n](其中m>0)的值域是[m,n],求a的取值范围;
(Ⅲ)解关于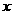 的不等式
的不等式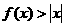 .
.
唐山市开滦一中2005–2006学年度第二次月考
21.(本题满分12分)已知数列 的前
的前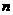 项和为
项和为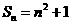 ,数列
,数列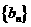 满足:
满足: ,
,
前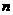 项和为
项和为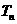 ,设
,设 .(
.( )
)
(Ⅰ) 求数列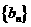 的通项公式;
的通项公式;
(Ⅱ)求证:数列 是单调递减数列;
是单调递减数列;
(Ⅲ)若对 时,总有
时,总有 成立,求正整数
成立,求正整数 的最小值.
的最小值.
20.(本小题满分12分) 已知圆M: ,直线L:
,直线L: ,过直线上一点A作△ABC,使∠BAC=45°,边AB过圆心M,且B、C在圆M上.
,过直线上一点A作△ABC,使∠BAC=45°,边AB过圆心M,且B、C在圆M上.
(Ⅰ) 当点A的横坐标为4,求直线AC的方程;
(Ⅱ)求点A的横坐标的取值范围.
19.(本小题满分12分)在 中,
中,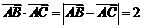 .
.
(Ⅰ)求 的值;(Ⅱ)若
的值;(Ⅱ)若 的面积为
的面积为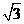 时,求
时,求 的值.
的值.
18. (本小题满分12分) 已知函数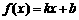 的图象与x、y轴分别相交于点A、B,
的图象与x、y轴分别相交于点A、B,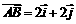 (
(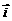 、
、 分别是与x、y轴正半轴同方向的单位向量), 函数
分别是与x、y轴正半轴同方向的单位向量), 函数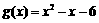 .
.
(Ⅰ) 求k、b的值;
(Ⅱ) 当x满足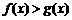 时,求不等式
时,求不等式 恒成立时
恒成立时 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com