

题目列表(包括答案和解析)
6.
方程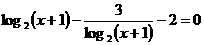 的解是
的解是 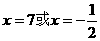 。
。
5.
函数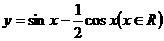 的最大值为
的最大值为 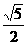 。
。
4.
设复数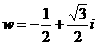 ,则
,则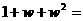
 。
。
3.
函数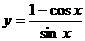 的最小正周期是
的最小正周期是 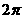 。
。
2.
已知集合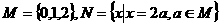 ,则集合
,则集合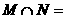
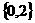 。
。
1.
函数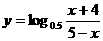 的定义域为
的定义域为 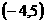 。
。
22、已知二次函数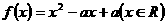 同时满足:①不等式
同时满足:①不等式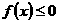 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在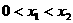 ,使得不等式
,使得不等式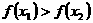 成立。
成立。
设数列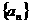 的前
的前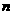 项和
项和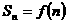 ,
,
(1)求数列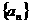 的通项公式;
的通项公式;
(2)试构造一个数列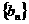 ,(写出
,(写出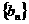 的一个通项公式)满足:对任意的正整数
的一个通项公式)满足:对任意的正整数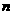 都有
都有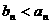 ,且
,且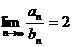 ,并说明理由;
,并说明理由;
(3)设各项均不为零的数列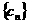 中,所有满足
中,所有满足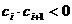 的正整数
的正整数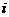 的个数称为这个数列
的个数称为这个数列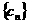 的变号数。令
的变号数。令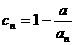 (
(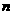 为正整数),求数列
为正整数),求数列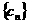 的变号数。
的变号数。
解:(1)∵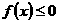 的解集有且只有一个元素,∴
的解集有且只有一个元素,∴ ,
,
当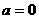 时,函数
时,函数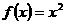 在
在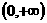 上递增,故不存在
上递增,故不存在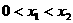 ,使得不等式
,使得不等式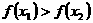 成立。
成立。
当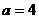 时,函数
时,函数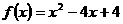 在
在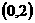 上递减,故存在
上递减,故存在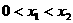 ,使得不等式
,使得不等式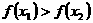 成立。
成立。
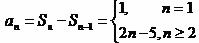 综上,得
综上,得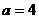 ,
,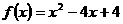 ,∴
,∴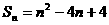 ,∴
,∴
(2)要使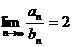 ,可构造数列
,可构造数列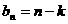 ,∵对任意的正整数
,∵对任意的正整数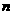 都有
都有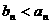 ,
,
∴当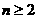 时,
时,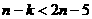 恒成立,即
恒成立,即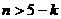 恒成立,即
恒成立,即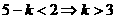 ,
,
又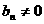 ,∴
,∴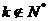 ,∴
,∴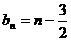 ,等等。
,等等。
(3)解法一:由题设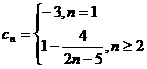 ,
,
∵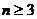 时,
时,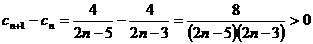 ,∴
,∴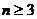 时,数列
时,数列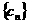 递增,
递增,
∵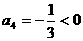 ,由
,由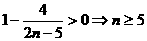 ,可知
,可知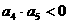 ,即
,即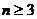 时,有且只有
时,有且只有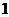 个变号数;
个变号数;
又∵ ,即
,即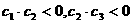 ,∴此处变号数有
,∴此处变号数有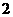 个。
个。
综上得 数列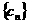 共有
共有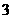 个变号数,即变号数为
个变号数,即变号数为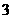 。
。
解法二:由题设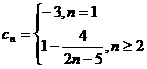 ,
,
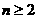 时,令
时,令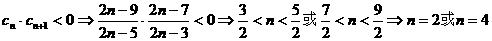 ;
;
又∵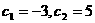 ,∴
,∴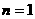 时也有
时也有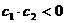 。
。
综上得 数列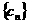 共有
共有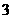 个变号数,即变号数为
个变号数,即变号数为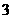 。
。
21、设函数 ,函数
,函数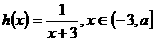 ,其中
,其中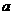 为常数且
为常数且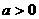 ,令函数
,令函数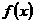 为函数
为函数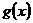 和
和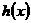 的积函数。
的积函数。
(1)求函数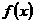 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当 时,求函数
时,求函数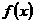 的值域;
的值域;
(3)是否存在自然数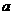 ,使得函数
,使得函数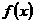 的值域恰为
的值域恰为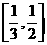 ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数 所构成的集合;若不存在,试说明理由。
所构成的集合;若不存在,试说明理由。
解:(1)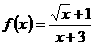 ,
,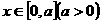 。
。
(2)∵ ,∴函数
,∴函数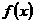 的定义域为
的定义域为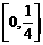 ,令
,令 ,则
,则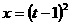 ,
,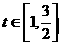 ,
,
∴ ,
,
∵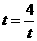 时,
时,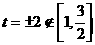 ,又
,又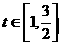 时,
时,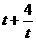 递减,∴
递减,∴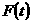 单调递增,
单调递增,
∴ ,即函数
,即函数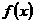 的值域为
的值域为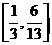 。
。
(3)假设存在这样的自然数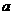 满足条件,令
满足条件,令 ,则
,则 ,
,
∵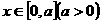 ,则
,则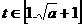 ,要满足值域为
,要满足值域为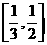 ,则要满足
,则要满足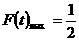 ,
,
由于当且仅当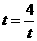
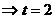 时,有
时,有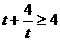 中的等号成立,且此时
中的等号成立,且此时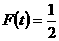 恰为最大值,
恰为最大值,
∴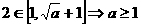 ,
,
又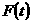 在
在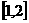 上是增函数,在
上是增函数,在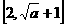 上是减函数,∴
上是减函数,∴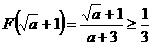
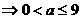 ,
,
综上,得 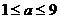 。
。
20、人口问题其实是许多国家的政府都要面对的问题。05年10月24日出版的《环球时报》就报道了一篇俄罗斯政府目前遭遇“人口危机”的文章。报道中引用了以下来自俄政府公布的数据:
●截至05年6月底,俄罗斯人口为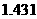 亿,人口密度每平方公里只有
亿,人口密度每平方公里只有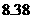 人;
人;
●04年一年俄人口就减少了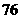 万,05年1月至5月共又减少了
万,05年1月至5月共又减少了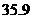 万;
万;
●据俄联邦安全会议预测,到2050年,俄将只有约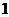 亿人口,比目前锐减
亿人口,比目前锐减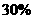 。
。
试根据以上数据信息回答下列问题:
(1)以04年至05年5月这17个月平均每月人口减少的数据为基础,假设每月人口减少相同,预测到2050年6月底,俄罗斯的人口约为多少亿?(保留三位小数)
(2)按第(1)小题给定的预测方法,到何时俄罗斯的人口密度将低于每平方公里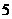 人?
人?
解:(1)由给出的信息可知,17个月里平均每月人口减少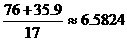 万人,
万人,
2005年6月底至2050年6月底共经过 个月,若每月人口减少数相同,
个月,若每月人口减少数相同,
则到2050年6月底俄罗斯的人口数约为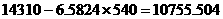 万,即约为
万,即约为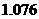 亿。
亿。
(2)设从05年6月底起,经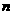 个月后俄罗斯的人口密度将低于每平方公里
个月后俄罗斯的人口密度将低于每平方公里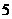 人,
人,
于是有 ,
,
∴至少要经过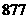 个月,即
个月,即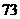 年零
年零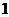 个月,也就是到2078年7月底,俄罗斯的人口密度将低于每平方公里
个月,也就是到2078年7月底,俄罗斯的人口密度将低于每平方公里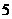 人。
人。
19、求证:不存在虚数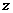 同时满足:①
同时满足:①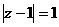 ;②
;②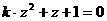 (
(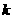 为实数且
为实数且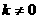 )。
)。
解:假设存在虚数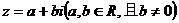 同时满足两个条件,
同时满足两个条件,
即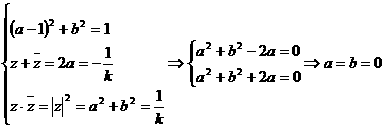 与假设
与假设 矛盾,
矛盾,
∴不存在虚数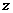 同时满足①②两个条件。
同时满足①②两个条件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com