
题目列表(包括答案和解析)
2、已知a,b为实数,集合M={,1},N={a,0},f:x→x表示把M中的元素x映射到集合N中仍为x,则a+b等于
A -1 B
-1 B 0 C
0 C 1 D
1 D ±1
±1
1、已知集合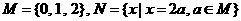 ,则集合
,则集合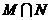 = ( )
= ( )
A.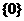 B.
B.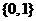 C.
C.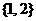 D.
D.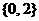
24.已知函数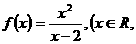 且
且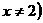
(1)求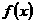 的单调区间;
的单调区间;
(2)若函数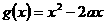 与函数
与函数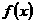 在
在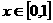 时有相同的值域,求
时有相同的值域,求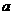 的值;
的值;
(3)设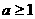 ,函数
,函数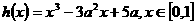 ,若对于任意
,若对于任意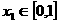 ,总存在
,总存在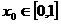 ,使得
,使得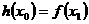 成立,求
成立,求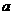 的取值范围。
的取值范围。
解:(1)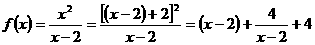 ,
,
易得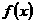 的单调递增区间为
的单调递增区间为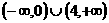 ;单调递减区间为
;单调递减区间为 。
。
(2)∵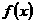 在
在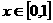 上单调递减,∴其值域为
上单调递减,∴其值域为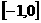 ,即
,即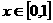 ,
,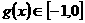 。
。
∵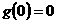 为最大值,∴最小值只能为
为最大值,∴最小值只能为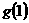 或
或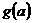 ,
,
若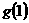
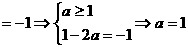 ;若
;若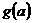
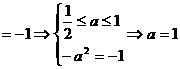 。综上得
。综上得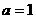 。
。
(3)设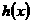 的值域为
的值域为 ,由题意知,
,由题意知,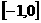

 。以下先证
。以下先证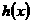 的单调性:设
的单调性:设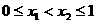 ,
,
∵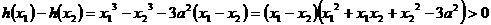 ,
,
(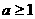
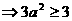 ,
,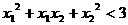 ), ∴
), ∴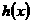 在
在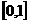 上单调递减。
上单调递减。
∴ , ∴
, ∴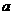 的取值范围是
的取值范围是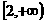 。
。
23.已知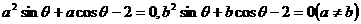 抛物线M的方程为
抛物线M的方程为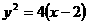
(1)求抛物线M的准线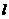 的方程;
的方程;
(2)求证:对任意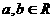 ,经过两点
,经过两点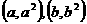 的直线与一定圆C想切,并求出圆C的方程;
的直线与一定圆C想切,并求出圆C的方程;
(3)设AB为定圆C的任意一条被直线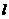 平分的弦,求证:所有这些弦所在的直线都与某一条抛物线有且仅有一个公共点。
平分的弦,求证:所有这些弦所在的直线都与某一条抛物线有且仅有一个公共点。
(1)解:抛物线M的准线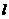 的方程为
的方程为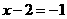 ,即
,即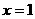 。
。
(2)证明:∵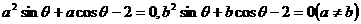 ,
,
∴经过两点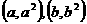 的直线方程为
的直线方程为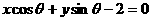 ,
,
∵原点到这条直线的距离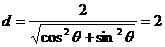 , ∴定圆C的方程为
, ∴定圆C的方程为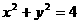 。
。
(3)证明:设AB与直线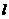 的交点为
的交点为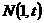 ,则
,则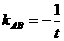 ,AB的方程为
,AB的方程为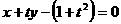 ,
,
由题意设抛物线方程为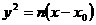 ,把
,把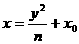 代入AB的方程,得
代入AB的方程,得
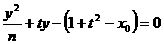 ,由
,由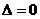 ,得
,得 ,
,
即所有这些弦所在的直线都与抛物线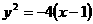 有且仅有一个公共点。
有且仅有一个公共点。
22、某银行准备新设一种定期存款业务,经预测,存款量与存款利率成正比,比例系数为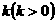 ,贷款的利率为6%,又银行吸收的存款能全部放贷出去。
,贷款的利率为6%,又银行吸收的存款能全部放贷出去。
(1)若存款的利率为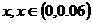 ,试分别写出存款数量
,试分别写出存款数量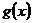 及银行应支付给储户的利息
及银行应支付给储户的利息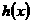 与存款利率
与存款利率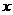 之间的关系式;
之间的关系式;
(2)存款利率定为多少时,银行可获得最大收益?
解:(1)存款量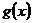
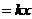 ,银行应支付的利息
,银行应支付的利息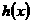
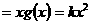 。
。
(2)设银行可获得收益为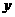 ,则
,则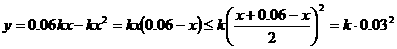 ,
,
当且仅当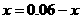 ,即
,即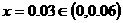 时取到最大值。
时取到最大值。
答:当存款利率定为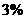 时,银行可获得最大收益。
时,银行可获得最大收益。
21、已知函数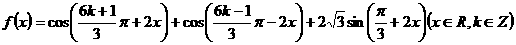
(1)求函数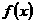 的最小正周期;
的最小正周期;
(2)求函数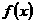 在
在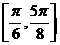 上的值域。
上的值域。
解:(1)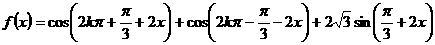
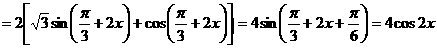
∴函数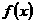 的最小正周期
的最小正周期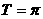 。
。
(2)∵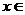
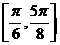 ,∴
,∴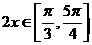 ,∴
,∴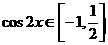 ,∴
,∴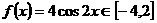 。
。
20、已知数列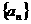 的首项是
的首项是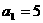 ,前
,前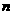 项和为
项和为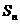 ,且
,且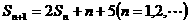 ,求数列
,求数列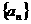 的通项公式。
的通项公式。
解: ,两式相减,得
,两式相减,得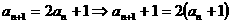 ,
,
∴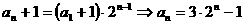 。
。
19、解不等式组: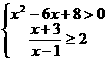
解: 。
。
18、已知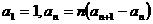 ,则数列
,则数列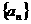 的通项公式
的通项公式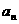 等于
( D )
等于
( D )
A、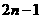 B、
B、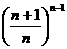 C、
C、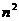 D、
D、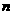
17、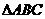 中,若
中,若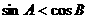 ,则
,则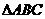 为
( C )
为
( C )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com