
题目列表(包括答案和解析)
3.没有函数f(x)=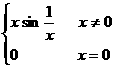
则f(x)在x=0处的性质是(B)
(A)连续且可导 (B)连续但不可导
(C)既不连续又不可导 (D)可导但不连续
填空题:
2.设f(x)在x0处可导,则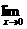
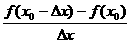 等于 (B)
等于 (B)
(A)f′(x0) (B)-f′(x0)
(C)f′(-x0) (D)不一定存在
1.设f′(x0),f′(0)均存在,以下四式中错误的一个是(D)
(A)f′(x0)=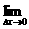
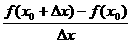
(B)f′(x0)=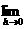
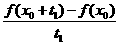
(C)f′(x0)=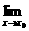
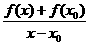
(D)f′(0)=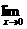
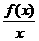
21、(本小题满分14分)
已知二次函数f(x)满足f(-1)=0,且 8x f(x)
f(x) 4(x2+1) 对
4(x2+1) 对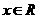 恒成立
恒成立
(1)求函数y=f(x)的解析式;
(2)利用函数g(x)=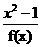 的定义域为D,构造一个数列{xn},方法如下:
的定义域为D,构造一个数列{xn},方法如下:
对于给定的定义域中的x1,令x2= g(x1),x3=g(x2),…,xn= g(xn-1),…
在上述构造过程中,如果xi(i=1,2,3,…)在定义域D中,构造数列的过程继续下去;如果xi不在定义域中,则构造数列的过程停止.
如果X1=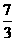 ,请求出满足上述条件的数列{xn}的集合M={x1,x2,…,xn}
,请求出满足上述条件的数列{xn}的集合M={x1,x2,…,xn}
19.(本小题满分14分)
已知点A(7,0)在曲线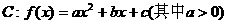 上,且曲线C在点A处的切线与直线
上,且曲线C在点A处的切线与直线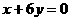 垂直,又当
垂直,又当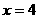 时,函数
时,函数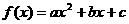 有最小值.
有最小值.
(I)求实数a,b,c的值;
(II)设函数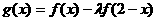 的最大值为M,
的最大值为M,
求正整数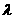 的值,使得
的值,使得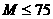 成立.
成立.
20(本小题满分14分)
函数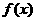 是定义域为R的偶函数,且对任意的
是定义域为R的偶函数,且对任意的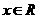 ,均有
,均有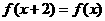 成立.当
成立.当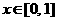 时,
时,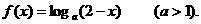
(1)当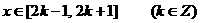 时,求
时,求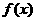 的表达式;
的表达式;
(2)若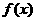 的最大值为
的最大值为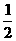 ,解关于x的不等式
,解关于x的不等式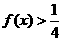 .
.
18. (本小题满分14分)


 通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,
讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随
后学生的注意力开始分散. 设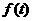 表示学生注意力随时间t(分钟)的变化规律(
表示学生注意力随时间t(分钟)的变化规律(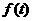
越大,表明学生注意力越集中),经过实验分析得知:

(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)有一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么
老师能否在学生达到所需的状态下讲授完这道题目?若能,老师如何安排讲解时
间;若不能,说明理由.
17、(本小题满分12分)
已知函数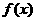 =
=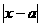 ,
,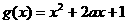 (a为正常数),
(a为正常数),
且函数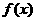 与
与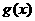 的图象在y轴上的截距相等.
的图象在y轴上的截距相等.
(1)求a的值;
(2)求函数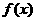 -
-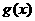 的单调递增区间.
的单调递增区间.
16、(本小题满分12分)
设函数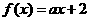 ,不等式
,不等式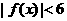 的解集为
的解集为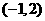 ,
,
试求不等式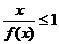 的解集
的解集
14、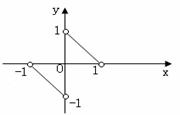 已知函数
已知函数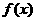 的图象如图,则不等式
的图象如图,则不等式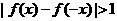 的解集为
。
的解集为
。
15已知x∈N*,f(x)= 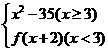 ,其值域设为D,给出下列数值:-26,-1,9,14,27,65,则其中属于集合D的元素是_________.
,其值域设为D,给出下列数值:-26,-1,9,14,27,65,则其中属于集合D的元素是_________.
(写出所有可能的数值)
13、已知函数y=f(x)的定义域是[0,2],且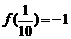 ,那么函数
,那么函数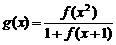 的定义域是_____________________
的定义域是_____________________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com