
题目列表(包括答案和解析)
4.已知随机变量的的分布列为
则DE等于( )
A.0 B.0.8 C.2 D.1
3.设15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为( )
A.15 B.10 C.20 D.5
|
ξ |
1 |
2 |
3 |
|
P |
0.4 |
0.2 |
0.4 |
2.设离散型随机变量ξ满足Eξ=-l,Dξ=3,则E[3(ξ-2)]等于( )
A.9 B.6 C.30 D.36
1.已知随机变量ξ服从二项分布ξ-B(n,P),且 Eξ=7,Dξ=6,则P等于( )
A.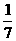 B.
B.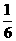 C.
C.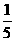 D.
D.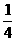
22.(本小题满分14分)
已知函数: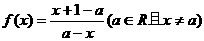
(1)求f(x)+f(2a-x)的值;
(2)当f(x)的定义域为[a+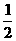 ,a+1]时,求f(x)的值域;
,a+1]时,求f(x)的值域;
(2)设函数g(x)=x2+|(x-a)f(x)| ,求g(x) 的最小值 .
21.(本小题满分12分)
设数列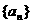 的首项a1=1,前n项和Sn满足关系
的首项a1=1,前n项和Sn满足关系
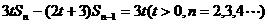 .
.
(1)求证:数列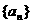 是等比数列;
是等比数列;
(2)设数列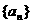 的公比是f(t),作数列
的公比是f(t),作数列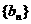 ,使
,使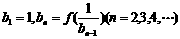 求bn;
求bn;
(3)求和: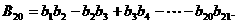
20.(本题满分12分)
如图,△AOE和△BOE都是边长为1的等边三角形,
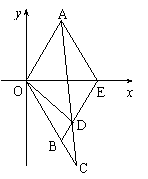 延长OB到C使|BC|=t(t>0),连AC交BE于D点.
延长OB到C使|BC|=t(t>0),连AC交BE于D点.
⑴用t表示向量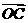 和
和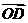 的坐标;
的坐标;
⑵当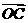 =
=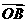 时,求向量
时,求向量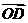 和
和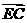 的夹角的大小.
的夹角的大小.
19.(本题满分12分)
已知函数f(x)=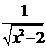 (x<-
(x<-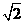 ),f(x)的反函数为g(x),点An(an,
),f(x)的反函数为g(x),点An(an,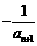 )在曲线y=g(x)上(n∈N+),且a1=1.
)在曲线y=g(x)上(n∈N+),且a1=1.
(1)求y=g(x)的表达式;
(2)求数列{an}的通项公式.
18.(本题满分12分)
函数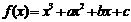 ,以曲线
,以曲线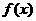 上的点
上的点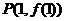 为切点的切线方程为
为切点的切线方程为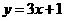 .
.
(1)若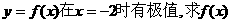 的表达式;
的表达式;
(2)在(1)的条件下,求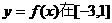 上的最大值.
上的最大值.
17、(本题满分12分)
已知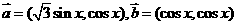 ,
,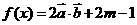 (
( ),
),
(1)求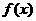 关于
关于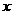 的表达式,并求
的表达式,并求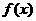 的最小正周期;
的最小正周期;
(2)若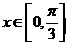 ,且
,且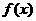 的最小值为5,求
的最小值为5,求 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com