
题目列表(包括答案和解析)
12、(本题满分12分)
解:(Ⅰ)令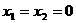 ,
,
依条件(3)可得f(0+0) ≥f(0)+f(0),即f(0) ≤0。
又由条件(1)得f(0) ≥0,则f(0)=0…………………… 3分
(Ⅱ)任取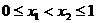 ,可知
,可知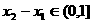
则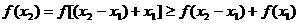 …………… 5分
…………… 5分
即 ,故
,故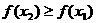
于是当0≤x≤1时,有f(x)≤f(1)=1
因此,当x=1时,f(x)有最大值为1,………………… 7分
(Ⅲ)证明:研究①当 时,f(x) ≤1<2x
时,f(x) ≤1<2x
②当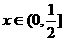 时,
时,
首先,f(2x) ≥f(x)+f(x)=2f(x),∴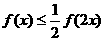 ………………9分
………………9分
显然,当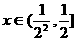 时,
时,
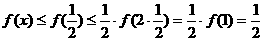 成立。
成立。
假设当 时,有
时,有 成立,其中k=1,2,…
成立,其中k=1,2,…
那么当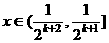 时,
时,
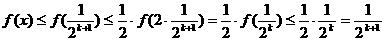
可知对于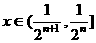 ,总有
,总有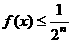 ,其中n=1,2,…
,其中n=1,2,…
而对于任意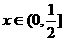 ,存在正整数n,使得
,存在正整数n,使得 ,
,
此时 …………………
…11分
…………………
…11分
③当x=0时,f(0)=0≤2x………… ……12分
综上可知,满足条件的函数f(x),对x∈[0,1],总有f(x) ≤2x成立。
11、(本题满分14分)
解:(Ⅰ)设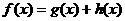 ①,其中
①,其中 是奇函数,
是奇函数,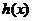 是偶函数,
是偶函数,
则有 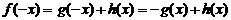 ②
②
联立①,②可得
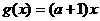 ,
,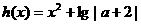 (直接给出这两个函数也给分)…3分
(直接给出这两个函数也给分)…3分
(Ⅱ)函数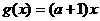 当且仅当
当且仅当 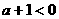 ,即
,即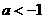 时才是减函数,
时才是减函数,
∴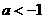
又
∴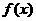 的递减区间是
的递减区间是 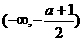 ……5分
……5分
由已知得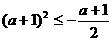
∴ 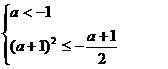 解得
解得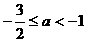
∴ 取值范围是
取值范围是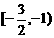 ……8分
……8分
(Ⅲ)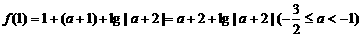
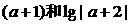 在
在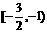 上为增函数 ……10分
上为增函数 ……10分
∴
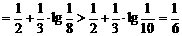
∴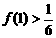 即
即 . ……14分
. ……14分
解: 当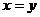 时,由已知不等式得
时,由已知不等式得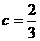 ……3分
……3分
下面分两部分给出证明:
⑴先证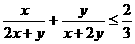 ,
,
此不等式
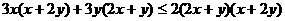
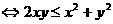 ,此式显然成立;
……7分
,此式显然成立;
……7分
⑵再证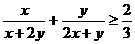 ,
,
此不等式
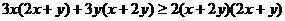
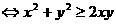 ,此式显然成立.
……10分
,此式显然成立.
……10分
综上可知,存在常数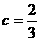 ,是对任意的整数x、y,题中的不等式成立.12分
,是对任意的整数x、y,题中的不等式成立.12分
10、(本题满分12分)
解:(1)记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1,乙为P2. (2分)
则P(A)=P1=0.6, P(B)=P2
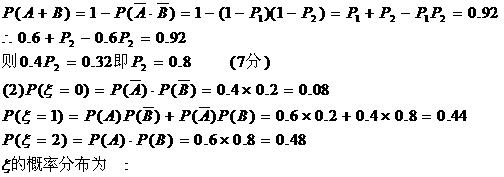
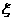 |
0 |
1 |
2 |
|
P |
0.08 |
0.44 |
0.48 |
14、(本小题满分14分)
(文科)已知椭圆C的中心在原点,焦点在x轴上,一条经过点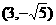 且方向向量为
且方向向量为
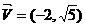 的直线l通过椭圆C的右焦点F,且交椭圆C于A、B两点,又
的直线l通过椭圆C的右焦点F,且交椭圆C于A、B两点,又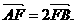
(1)求直线l的方程; (2)求椭圆C的方程.
(理科)已知椭圆C的中心在原点,焦点在x轴上,一条经过点(3,-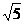 )且方向向量为
)且方向向量为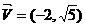 的直线l交椭圆C于A、B两点,交x轴于M点,又
的直线l交椭圆C于A、B两点,交x轴于M点,又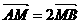 .
.
(1)求直线l方程; (2)求椭圆C长轴长取值的范围.
培优练习(1)答案
13、(本小题满分16分)
在直角坐标平面内,已知两点A(-2,0)及B(2,0),动点Q到点A的距离为6,线段BQ的垂直平分线交AQ于点P。
(Ⅰ)证明|PA|+|PB|为常数,并写出点P的轨迹T的方程;
 (Ⅱ)过点B的直线l与曲线T相交于M、N两点,线段MN的中点R与点S(-1,0)的连线的纵截距为t,试求t 的取值范围。
(Ⅱ)过点B的直线l与曲线T相交于M、N两点,线段MN的中点R与点S(-1,0)的连线的纵截距为t,试求t 的取值范围。
12、(本小题满分12分)
已知定义域为[0,1]的函数f (x)同时满足:
(1)对于任意x∈[0,1],总有f (x)≥0;
(2)f (1) =1;
(3)若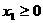 ,
,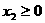 ,
,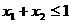 ,则有
,则有 。
。
(Ⅰ)试求f(0)的值;
(Ⅱ)试求函数f(x)的最大值;
(Ⅲ)试证明:满足上述条件的函数f(x)对一切实数x,都有f(x)≤2x 。
11、(本小题满分14分)
已知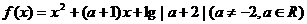
(Ⅰ)若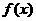 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数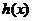 的和,求
的和,求 和
和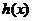
的解析式;
(Ⅱ)若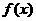 和
和 在区间
在区间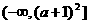 上都是减函数,求a的取值范
上都是减函数,求a的取值范
(Ⅲ)在(Ⅱ)的条件下,比较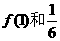 的大小.
的大小.
10、(本小题满分12分)
甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92.
(1)求该题被乙独立解出的概率;(2)求解出该题的人数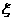 的数学期望和方差.
的数学期望和方差.
9、(本小题满分12分)
是否存在常数c,使得不等式 对任意正实数x、y恒成立?证明你的结论.
对任意正实数x、y恒成立?证明你的结论.
8、如图,矩形ABCD中,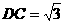 ,AD=1,在DC上截取DE=1,将△ADE沿AE翻折到
,AD=1,在DC上截取DE=1,将△ADE沿AE翻折到
 D′点,当D′在平面ABC上的射影落在AE上时,四棱锥D′-ABCE的体积是________;当D′在平面ABC上的射影落在AC上时,二面角D′-AE-B的平面角的余弦值是_________。
D′点,当D′在平面ABC上的射影落在AE上时,四棱锥D′-ABCE的体积是________;当D′在平面ABC上的射影落在AC上时,二面角D′-AE-B的平面角的余弦值是_________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com