
题目列表(包括答案和解析)
8.已知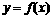 定义域为
定义域为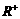 ,且对任意的
,且对任意的 、
、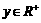 ,恒有
,恒有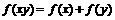 ,
,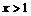 时,
时,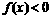 .
.
(1)求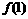 的值,并证明
的值,并证明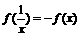 ;
;
(2)求证:在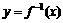 的定义域内恒有
的定义域内恒有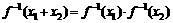 .
.
7. 绿缘商店每月向工厂按出厂价每瓶3元购进一种饮料。根据以前的统计数据,若零售价定为每瓶4元,每月可销售400瓶;若每瓶售价每降低0.05元,则可多销售40瓶。请你给该商店设计一个方案:每月的进货量当月销售完,销售价应定为多少元和从工厂购进多少瓶时,才可获得最大的利润?
6.已知函数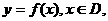
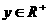 ,且正数C为常数.对于任意的
,且正数C为常数.对于任意的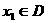 ,存在一个
,存在一个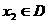 ,使
,使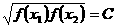 ,则称函数
,则称函数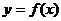 在D上的均值为C. 试依据上述定义,写出一个均值为9的函数的例子:________________.
在D上的均值为C. 试依据上述定义,写出一个均值为9的函数的例子:________________.
5.偶函数 在
在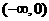 上单调递增,则
上单调递增,则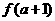 与
与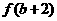 的大小关系是 ( )
的大小关系是 ( )
(A)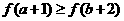 (B)
(B)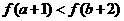
(C)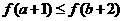 (D)
(D)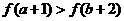
4.定义两种运算: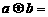
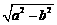 ,
,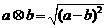 ,则函数
,则函数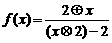 为( )
为( )
(A)奇函数 (B)偶函数
(C)奇函数且为偶函数 (D)非奇函数且非偶函数
3.某天清晨,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常,但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了. 下面大致能上反映出小鹏这一天(0时-24时)体温的变化情况的图是 ( )

(A ) (B) (C) (D)
2.已知集合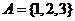 ,
,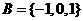 ,则满足条件
,则满足条件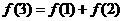 的映射
的映射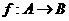 的个数是 ( )
的个数是 ( )
(A)2 (B)4 (C)5 (D)7
1.合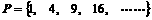 ,若
,若 ,
,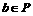 ,则
,则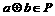 ,则运算
,则运算 可能是 ( )
可能是 ( )
(A)加法 (B)减法 (C) 除法 (D)乘法
22.(本题14分)(文)已知A、B、D三点不在一条直线上,且A(-2 ,0) ,
B(2 ,0),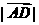 = 2 ,
= 2 ,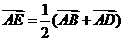
(1)求点E的轨迹方程;
(2)过点A作直线L交以A、B为焦点的椭圆于M、N两点。线段MN的中点到y轴距离为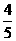 且直线MN与点E的轨迹相切,求椭圆的方程.
且直线MN与点E的轨迹相切,求椭圆的方程.
(理)在直角坐标平面中,△ABC的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M同时满足①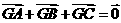 , ②
, ②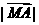 =
= 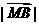 =
=  ③
③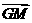 ∥
∥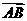
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为(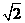 , 0) ,已知
, 0) ,已知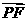 ∥
∥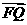 ,
, 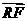 ∥
∥ 且
且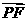 ·
·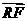 = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.
|
21.(本题12分)(文)已知函数f (x)
= a·bx的图像过点A(1, 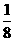 ), B (2 ,
), B (2 , 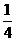 )
)
(1 ) 求函数f ( x ) 的解析式.
(2)设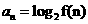 , n∈N+, Sn 是数列
, n∈N+, Sn 是数列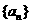 前n项和,求S20.
前n项和,求S20.
(3)在(2 )的条件下,若 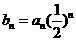 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(理)已知数列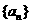 中各项为:
中各项为:
|
|
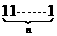
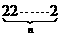 ……
……
(1)证明这个数列中的每一项都是两个相邻整数的积.
(2)求这个数列前n项之和Sn .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com