
题目列表(包括答案和解析)
5. 某地为了防止水土流失,植树造林,绿化荒沙地,每年比上一年多植相同亩数的林木,但由于自然环境和人为因素的影响,每年都有相同亩数的土地沙化,具体情况为下表所示:
|
|
1998年 |
1999年 |
2000年 |
|
新植亩数 |
1000 |
1400 |
1800 |
|
沙地亩数 |
25200 |
24000 |
22400 |
而一旦植完,则不会被沙化.
问:(1)每年沙化的亩数为多少?
(2)到那一年可绿化完全部荒沙地?
4. 设数列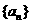 的前n项和为
的前n项和为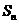 ,令
,令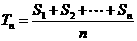 ,称
,称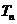 为数列
为数列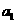 ,
,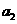 ,……,
,……,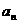 的“理想数”,已知数列
的“理想数”,已知数列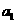 ,
,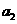 ,……,
,……,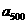 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 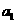 ,
,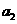 ,……,
,……,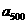 的“理想数”为
的“理想数”为
(A) 2002 (B) 2004 (C) 2006 (D) 2008
3. 2003年12月,全世界爆发"禽流感",科学家经过深入的研究,终于发现了一种细菌M在杀死"禽流感"病毒N的同时能够自身复制.已知1个细菌M可以杀死1个病毒N,并且生成2个细菌M,那么1个细菌M和2048个"禽流感"病毒N最多可生成细菌M的数值是 ( )
(A)1024 (B)2048 (C) 2049 (D)无法确定
2. 若等比数列的各项均为正数,前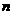 项之和为
项之和为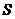 ,前
,前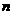 项之积为
项之积为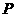 ,前
,前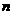 项倒数之和为
项倒数之和为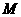 ,则
( )
,则
( )
(A)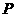 =
=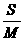 (B)
(B)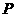 >
>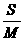 (C)
(C)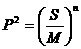 (D)
(D)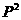 >
>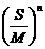
10. (1)假设有两个不同的点(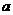 ,
,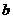 ),(
),(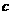 ,
,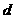 )对应同一函数,即
)对应同一函数,即 与
与 相同,
相同,
即 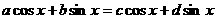 对一切实数x均成立。
对一切实数x均成立。
特别令x=0,得a=c;令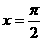 ,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
故不存在两个不同点对应同函数。
(2)当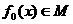 时,可得常数a0,b0,使
时,可得常数a0,b0,使
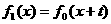
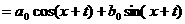
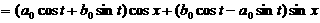 。
。
由于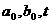 为常数,设
为常数,设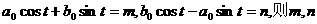 是常数.
是常数.
从而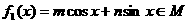 。
。
(3)设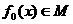 ,由此得
,由此得
( ,
,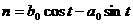 )
)
在映射F下,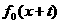 的原象是(m,n),则M1的原象是
的原象是(m,n),则M1的原象是
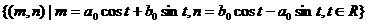
消去t得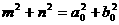 ,即在映射F下,M1的原象
,即在映射F下,M1的原象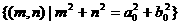 是以原点为圆心,
是以原点为圆心,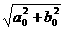 为半径的圆.
为半径的圆.
第二讲 数列
陕西特级教师 安振平
l 高考风向标
数列的概念.等差数列及其通项公式、前n项和公式;等比数列及其通项公式、前n项和公式.数学归纳法及其应用.通项与前n项和之间的关系是高考常考的热点内容,递推数列在各地的高考中闪亮登场.
l 典型题选讲
例1 若数列{an}满足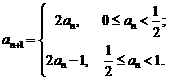 若
若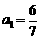 ,则
,则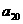 的值为 ( )
的值为 ( )
A.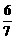 B.
B. C.
C. D.
D.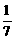
讲解 逐步计算,可得
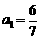 ,
,
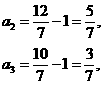
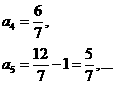
这说明数列{an}是周期数列,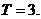 而
而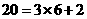 , 所以
, 所以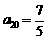 .应选B.
.应选B.
点评 分段数列问题是一种新问题,又涉及到周期数列,显示了以能力立意,题活而不难的特色.
例2 在等比数列{an}中,前n项和为Sn,若Sm,Sm+2,Sm+1成等差数列,则am, am+2, am+1成等差数列.
(1)写出这个命题的逆命题;
(2)判断逆命题是否为真,并给出证明.
讲解 (1)逆命题:在等比数列{an}中,前n项和为Sn,若am, am+2, am+1成等差数列,则 Sm,Sm+2,Sm+1成等差数列.
(2)设{an}的首项为a1,公比为q
由已知得2am+2= am
+ am+1
∴2a1qm+1=a1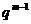 +a1qm
+a1qm
∵a1≠0 q≠0 ,
∴2q2-q-1=0 ,
∴q=1或q=-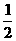 .
.
当q=1时,
∵Sm=ma1, Sm+2= (m+2)a1,Sm+1= (m+1)a1,
∴Sm+Sm+1≠2 Sm+2,
∴Sm,Sm+2,Sm+1不成等差数列.
当q=-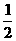 时,
时,
2 Sm+2=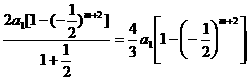 ,
,
∴Sm+Sm+1=2 Sm+2 ,
∴Sm,Sm+2,Sm+1成等差数列.
综上得:当公比q=1时,逆命题为假;
当公比q≠1时,逆命题为真.
点评 对公比进行分类是本题解题的要害所在,问题好在分类,活在逆命题亦假亦真二者兼顾,可谓是一道以知识呈现、能力立意的新颖试题.
例3 设数列{an}前n的项和为 Sn,且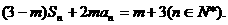 其中m为常数,
其中m为常数,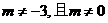
(1)求证:{an}是等比数列;
(2)若数列{an}的公比满足q=f(m)且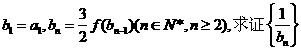 ,为等差数列,并求
,为等差数列,并求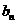 .
.
讲解(1)由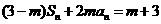 ,得
,得
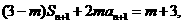
两式相减,得
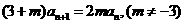
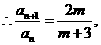
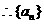 是等比数列.
是等比数列.

点评 为了求数列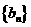 的通项,用取"倒数"的技巧,得出数列
的通项,用取"倒数"的技巧,得出数列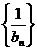 的递推公式,从而将其转化为等差数列的问题.
的递推公式,从而将其转化为等差数列的问题.
例4 设数列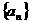 的前n项和为Sn,若
的前n项和为Sn,若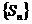 是首项为S1各项均为正数且公比为q的等比数列.
是首项为S1各项均为正数且公比为q的等比数列.
(1)求数列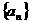 的通项公式
的通项公式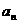 (用S1和q表示);
(用S1和q表示);
(2)试比较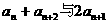 的大小,并证明你的结论.
的大小,并证明你的结论.
讲解 (1)∵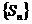 是各项均为正数的等比数列,
是各项均为正数的等比数列,
∴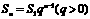 .
.
当n=1时,a1=S1;
当 .
.
∴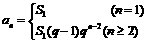
(2)当n=1时,
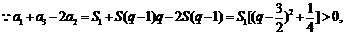
∴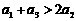 .
.
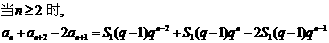
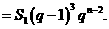
∵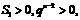
①当q=1时,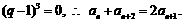
②当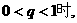
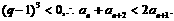
③当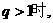
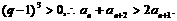
综上以上,我们可知:当n=1时,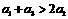 .当
.当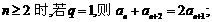
若 若
若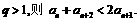
点评 数列与比较大小的综合是高考命题的一个老话题,我们可以找到较好的高考真题.本题求解当中用到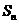 与
与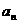 之间的关系式:
之间的关系式:

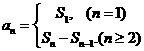
例5 已知数列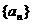 满足
满足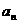 >0,且对一切n∈N*,有
>0,且对一切n∈N*,有 ,
,
(1) 求证:对一切n∈N*,有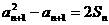 ;
;
(2) 求数列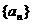 的通项公式;
的通项公式;
(3) 求证: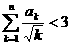 .
.
讲解 (1) 由 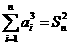 ①
①
得 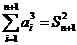 ②
②
②-①得 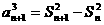 =(Sn+1+Sn)(Sn+1-Sn)=(2
Sn+an+1) an+1
=(Sn+1+Sn)(Sn+1-Sn)=(2
Sn+an+1) an+1
∵ an+1 >0,
∴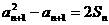 .
.
(2)
由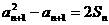 ,得
,得
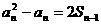 (n≥2),
(n≥2),
两式相减,得
(an+1+ an)( an+1 - an)= an+1+ an,
∵an+1+ an >0,
∴an+1 - an =1.(n≥2)
当n=1,2时易得,a1=1,a2=2,∴an+1 - an =1(n≥1) .
从而{ an}是等差数列,其首项为a1=1,公差d=1,故an=n .
(3) 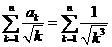
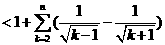
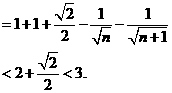
点评 关于数列不等式的证明,常用的技巧是放缩法,而放缩应特别注意其适度性,不可过大,也不可过小.
例6 如图,一粒子在区域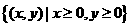 上运动,在第一秒内它从原点运动到点
上运动,在第一秒内它从原点运动到点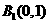 ,接着按图中箭头所示方向在x轴、y轴及其平行方向上运动,且每秒移动一个单位长度.
,接着按图中箭头所示方向在x轴、y轴及其平行方向上运动,且每秒移动一个单位长度.
(1)设粒子从原点到达点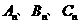 时,所经过的时间分别为
时,所经过的时间分别为 ,试写出
,试写出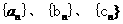 的通相公式;
的通相公式;
(2)求粒子从原点运动到点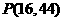 时所需的时间;
时所需的时间;
(3)粒子从原点开始运动,求经过2004秒后,它所处的坐标.
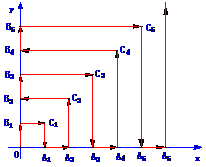 讲解 (1) 由图形可设
讲解 (1) 由图形可设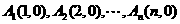 ,当粒子从原点到达
,当粒子从原点到达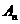 时,明显有
时,明显有
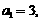
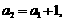
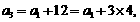
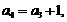
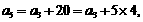
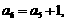
… …
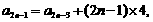
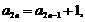
∴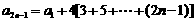 =
=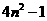 ,
,
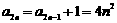 .
.
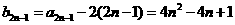 ,
,
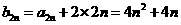 .
.
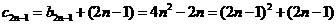 ,
,
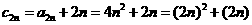 ,
,
即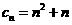 .
.
(2)有图形知,粒子从原点运动到点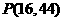 时所需的时间是到达点
时所需的时间是到达点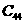 所经过得时间
所经过得时间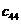 再加(44-16)=28秒,所以
再加(44-16)=28秒,所以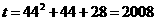 秒.
秒.
(3)由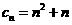
 2004,解得
2004,解得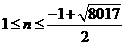 ,取最大得n=44,
,取最大得n=44,
经计算,得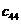 =1980<2004,从而粒子从原点开始运动,经过1980秒后到达点
=1980<2004,从而粒子从原点开始运动,经过1980秒后到达点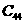 ,再向左运行24秒所到达的点的坐标为(20,44).
,再向左运行24秒所到达的点的坐标为(20,44).
点评 从起始项入手,逐步展开解题思维.由特殊到一般,探索出数列的递推关系式,这是解答数列问题一般方法,也是历年高考命题的热点所在.
例7 已知数列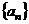 的前
的前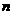 项和
项和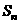 满足
满足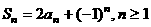 .
.
(1)写出数列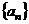 的前三项
的前三项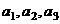 ;
;
(2)求数列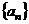 的通项公式;
的通项公式;
(3)证明:对任意的整数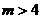 ,有
,有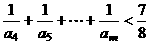 .
.
讲解 (1)为了计算前三项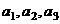 的值,只要在递推式
的值,只要在递推式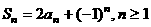 中,对
中,对 取特殊值
取特殊值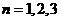 ,就可以消除解题目标与题设条件之间的差异.
,就可以消除解题目标与题设条件之间的差异.
由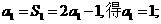
由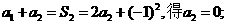
由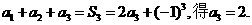
(2)为了求出通项公式,应先消除条件式中的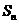 .事实上
.事实上
当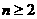 时,有
时,有
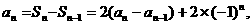
即有 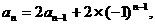
从而 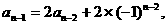
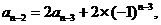
……
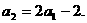
接下来,逐步迭代就有
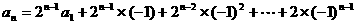
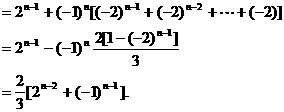
经验证a1也满足上式,故知 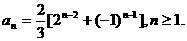
其实,将关系式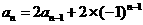 和课本习题
和课本习题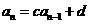 作联系,容易想到:这种差异的消除,只要对
作联系,容易想到:这种差异的消除,只要对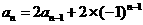 的两边同除以
的两边同除以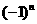 ,便得
,便得
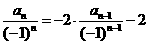 .
.
令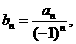 就有
就有
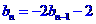 ,
,
于是
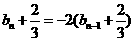 ,
,
这说明数列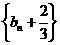 是等比数列,公比
是等比数列,公比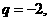 首项
首项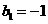 ,从而,得
,从而,得
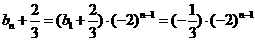 ,
,
即 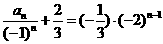 ,
,
故有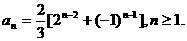
(3)由通项公式得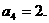
当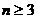 且n为奇数时,
且n为奇数时, 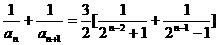
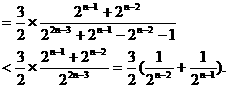
当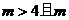 为偶数时,
为偶数时,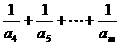
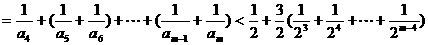
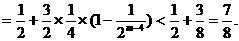
当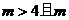 为奇数时,
为奇数时,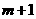 为偶数,可以转化为上面的情景
为偶数,可以转化为上面的情景
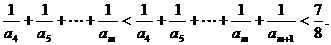
故任意整数m>4,有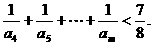
点评 本小题2004年全国(旧教材版)高考理科压轴试题.主要考查数列的通项公式,等比数列的前n项和以及不等式的证明.考查灵活运用数学知识分析问题和解决问题的能力.当中的第2小题,显然与课本上的问题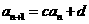 有着相同的本质.而第3小题又有着明显的高等数学的背景,体现了知识与技能的交汇,方法与能力的提升,显示了较强的选拔功能.
有着相同的本质.而第3小题又有着明显的高等数学的背景,体现了知识与技能的交汇,方法与能力的提升,显示了较强的选拔功能.
l 针对性演练
1 某人要买房,随着楼层的升高,上下楼耗费的精力增多,因此不满意度升高,当住第n层楼时,上下楼造成的不满意度为n,但高处空气清新,嘈杂音较小,环境较为安静,因此随楼层升高环境不满意度降低,设住第n层楼时,环境不满意度为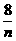 ,则此人应选( )
,则此人应选( )
(A) 1楼 (B) 2楼 (C) 3楼 (D) 4楼
9.(I)令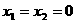 ,
,
依条件(3)可得f(0+0) ≥f(0)+f(0),即f(0) ≤0.
又由条件(1)得f(0) ≥0,则f(0)=0.
(Ⅱ)任取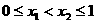 ,可知
,可知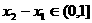 ,
,
则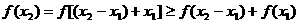 ,
,
即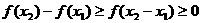 ,故
,故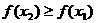
于是当0≤x≤1时,有f(x)≤f(1)=1
因此,当x=1时,f(x)有最大值为1,
(Ⅲ)证明:
研究①当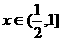 时,f(x) ≤1<2x
时,f(x) ≤1<2x
②当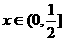 时,
时,
首先,f(2x) ≥f(x)+f(x)=2f(x),∴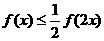 .
.
显然,当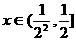 时,
时,
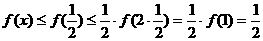 成立.
成立.
假设当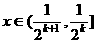 时,有
时,有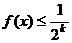 成立,其中k=1,2,…
成立,其中k=1,2,…
那么当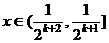 时,
时,

可知对于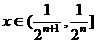 ,总有
,总有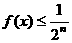 ,其中n=1,2,…
,其中n=1,2,…
而对于任意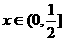 ,存在正整数n,使得
,存在正整数n,使得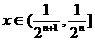 ,
,
此时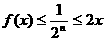 ,
,
③当x=0时,f(0)=0≤2x..
综上可知,满足条件的函数f(x),对x∈[0,1],总有f(x) ≤2x成立.
7.450.8.略.
1.D.2.D.3.C.4.A.5.D.6.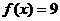 ,
,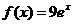 ,
, 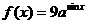 (
(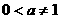 ).
).
10. 设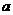 、
、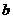 为常数,
为常数,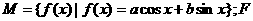 :把平面上任意一点
:把平面上任意一点
(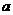 ,
,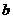 )映射为函数
)映射为函数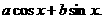
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当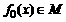 时,
时,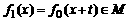 ,这里t为常数;
,这里t为常数;
(3)对于属于M的一个固定值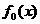 ,得
,得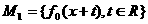 ,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象?
,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象?
答案:
9.已知定义域为[0,1]的函数f(x)同时满足:
(1)对于任意x∈[0,1],总有f(x)≥0;
(2)f(1)=1
(3)若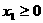 ,
,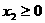 ,
,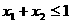 ,则有
,则有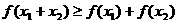
(Ⅰ)试求f(0)的值;
(Ⅱ)试求函数f(x)的最大值;
(Ⅲ)试证明:满足上述条件的函数f(x)对一切实数x,都有f(x)≤2x..
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com