
题目列表(包括答案和解析)
2.在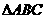 中,若
中,若 为钝角,则tan A·tan B的值为(*)
为钝角,则tan A·tan B的值为(*)
(A)小于1 (B) 等于1 (C) 大于1 (D) 不能确定
1.已知集合P={ 0,m},Q={x│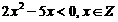 },若P∩Q
≠
},若P∩Q
≠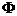 ,则m等于 (*)
,则m等于 (*)
(A) 1
(B)
2
(C)
1或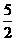 (D)1或2
(D)1或2
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P. 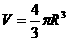
那么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径

22、(本小题满分12分)平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,
-2),点C满足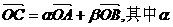 、
、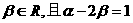
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线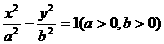 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: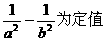 .
.
21、(本小题满分12分)如图,在底面是菱形的四棱锥P-ABCD中,
∠ABC=600,PA=AC=a,PB=PD=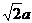 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(1)证明PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角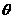 的大小;
的大小;
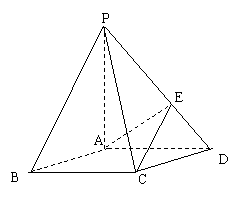 (3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
(3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
20、(本大题满分12分)
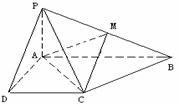 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,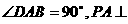 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=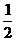 AB=1,M是PB的中点。
AB=1,M是PB的中点。
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小。
19、(本大题满分14分)已知a=(cosα,sinα),b=(cosβ,sinβ)(0<α<β<π),
(1)求证: a+b与a-b互相垂直;
(2)若ka+b与a-kb的大小相等(k∈R且k≠0),求β-α
18、若非零向量α、β满足|α+β|=|α-β|,则α与β所成角的大小为_____.
17、已知向量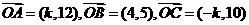 ,且A、B、C三点共线,则k=
,且A、B、C三点共线,则k=
16、已知平面上三点A、B、C满足 =3,
=3, 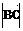 =4,
=4, 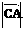 =5,则
=5,则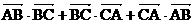 的值等于__________。
的值等于__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com