
题目列表(包括答案和解析)
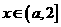 时,
时,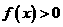 ,
,
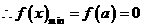 ;
;
20.(本小题满分12分)
(理)已知a>1,函数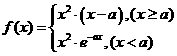 ,求函数f(x)在
,求函数f(x)在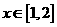 时的最小值。
时的最小值。
解:一.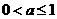 时,
时,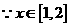 ,
,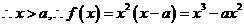 ,
,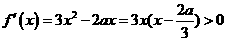 ,
,
 时是增函数,
时是增函数,
 ;
;
19.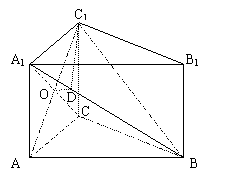 解法(一):(1)在△ABC中
解法(一):(1)在△ABC中
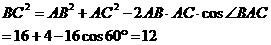
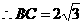
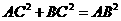
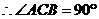 ,即
,即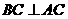 ,
,
由直三棱柱性质知:平面ACC1A1⊥平面ABC。
∴BC⊥平面ACC1A1
∴BC⊥A1C 又BC∥B1C1
∴B1C1⊥A1C ……………………………………………………………… 4分
(2)∵BC∥B1C1,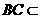 平面ABC,
平面ABC,
∴B1C1∥平面A1CB
∴B1点到平面A1CB的距离等于点C1到平面A1CB的距离。……………………6分
设点B1点到平面A1CB的距离为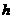 ,则
,则

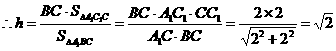 ………………………8分
………………………8分
(3)连结AC1,交A1C于O,过O作OD⊥A1B于D,连结C1D
由(1)BC⊥平面ACC1A1得:平面BCA1⊥平面ACC1A1
由正方形ACC1A1知AC1⊥A1C
∴C1A⊥平面A1BC
∴OD是C1D在平面A1BC上的射影
∴C1D⊥A1B(三垂线定理)
∴∠ODC1是二面角C1-A1B-C的平面角。……………………………………10分
在△A1BC中,A1B=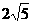 ,BC=
,BC=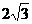 ,A1C=
,A1C=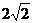 ,A1O=
,A1O=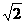 。
。
由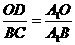 得:
得: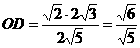
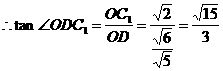
∴二面角C1-A1B-C的大小是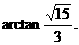 ……………………………………12分
……………………………………12分
解法(二)先证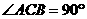 ,然后以C为原点,分别以CA、CB、CC1为
,然后以C为原点,分别以CA、CB、CC1为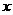 轴、
轴、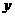 轴、
轴、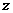 轴建立空间直角坐标系(略)
轴建立空间直角坐标系(略)
19. (本小题满分12分)
(本小题满分12分)
已知直三棱柱ABC-A1B1C1中,AB= 4,AC=AA1=2,∠CAB=60°。
(1) 求证:A1C⊥B1C1;
(2) 求点B1到平面A1BC的距离;
(3) 求二面角C1-A1B-C的大小。
18. (本小题满分12分)
某人抛掷一枚硬币,出现正反的概率都是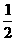 ,构造数列
,构造数列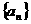 ,使得
,使得 ,记
,记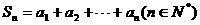 。
。
(1)
求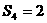 的概率;
的概率;
(2)
求:前两次均出现正面,且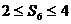 的概率。
的概率。
(3)
(理科做文科不做)记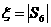 ,求
,求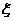 的数学期望。
的数学期望。
解:(1)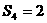 ,需4次中有3次正面1次反面,设其概率为
,需4次中有3次正面1次反面,设其概率为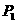
则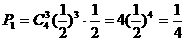
(2)6次中前两次均出现正面,要使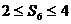 ,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为
,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为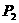 。
。
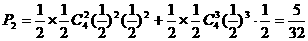
(3)6次中前两次均出现正面,记后4次中出现正面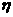 次,则
次,则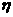
 -B(4,
-B(4,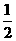 ),
),
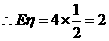 ,
,
又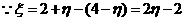 ,
,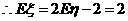 。
。
17.(本小题满分12分)
已知: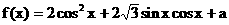 (
(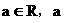 为常数)
为常数)
(I)若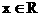 ,求
,求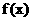 的最小正周期;
的最小正周期;
(II)若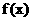 在
在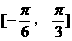 上最大值与最小值之和为3,求a的值。
上最大值与最小值之和为3,求a的值。
解: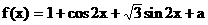 ……3分
……3分
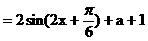 ……5分
……5分
(I)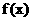 的最小正周期
的最小正周期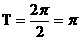 ……6分
……6分
(II)由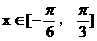 知
知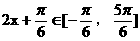 ……8分
……8分
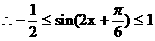
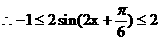 ……10分
……10分
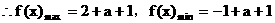
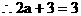 ,解得
,解得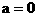 ……12分
……12分
16.(1)斜面的中面面积等于斜面面积的四分之一;(2)三个直角面面积的平方和等于斜面面积的平方;(3)斜面与三个直角面所成二面角的余弦平方和等于1.
16.将侧棱相互垂直的三棱锥称为“直角三棱锥”,三棱锥的侧面和底面分别叫为直角三棱锥的“直角面和斜面”;过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”.请仿照直角三角形以下性质:(1)斜边的中线长等于斜边边长的一半;(2)两条直角边边长的平方和等于斜边边长的平方;(3)斜边与两条直角边所成角的余弦平方和等于1.
写出直角三棱锥相应性质(至少一条): .
15.已知变量x、y满足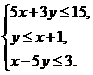 ,若使z=x+ky最小的最优解有无穷多个,则k的值是__-1____。
,若使z=x+ky最小的最优解有无穷多个,则k的值是__-1____。
11.函数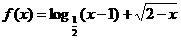 的定义域为_
的定义域为_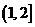 ;值域为
;值域为 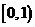 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com