
题目列表(包括答案和解析)
13 14
15 16
22、(本小题满分12分)
设函数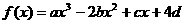 (a、b、c、d∈R)图象关于原点对称,且x=1时,
(a、b、c、d∈R)图象关于原点对称,且x=1时,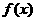 取极小值
取极小值
(1)求a、b、c、d的值;
(2)当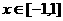 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
(3)若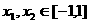 时,求证:
时,求证: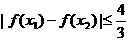 .
.
座位号:
 昆明一中2005-2006学年度上学期期末高三一轮复习终结测试
昆明一中2005-2006学年度上学期期末高三一轮复习终结测试
数学试卷(理科)答题卷 2006.1
第Ⅱ卷(非选择题,共90分)
21、(本小题满分14分)
已知F1(-2,0),F2(2,0)是椭圆C的两个焦点,过F1的直线与椭圆C的两个交点为M,N,且| MN |的最小值为6.
(I)求椭圆C的方程;
(II)设A,B为椭圆C的长轴顶点.当|MN|取最小值时,求∠AMB的大小.
20、(本小题满分12分)
已知数列{an}满足:a1=-,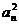 +(an+1+2)an+2an+1+1=0。求证:
+(an+1+2)an+2an+1+1=0。求证:
(1)-1<an<0;
(2)a2n>a2n-1对一切n∈N*都成立;
(3)数列{ a2n-1}为递增数列.
19、(本小题满分12分)
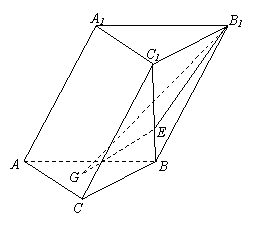 如图,在斜三棱柱
如图,在斜三棱柱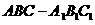 中,侧面
中,侧面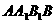 ⊥底面
⊥底面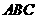 ,侧棱
,侧棱 与底面
与底面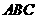 成60°的角,
成60°的角,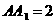 ,底面
,底面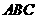 是边长为2的正三角形,其重心为
是边长为2的正三角形,其重心为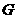 点.
点.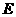 是线段
是线段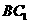 上一点,且
上一点,且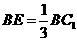 .
.
⑴求证: ∥侧面
∥侧面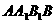 ;
;
⑵求平面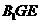 与底面
与底面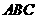 所成锐角二面角的大小.
所成锐角二面角的大小.
18、(本小题满分12分)
下表是某班英语及数学成绩的分布表,已知该班有50名学生,成绩分1至5个档次。如表中所示英语成绩为4分,数学成绩为2分的学生有5人,现设该班任意一位学生的英语成绩为 ,数学成绩为
,数学成绩为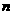
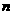  |
数学 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
英语 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
9 |
3 |
|
|
2 |
1 |
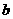 |
6 |
0 |
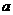 |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
(1)求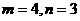 的概率;(2)求在
的概率;(2)求在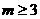 的条件下,
的条件下,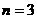 的概率;
的概率;
(3)求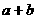 的值,并求
的值,并求 的数学期望;
的数学期望;
(4)若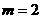 与
与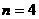 是相互独立的,求
是相互独立的,求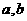 的值;
的值;
17、(本小题满分12分)
已知定义在R上的函数f(x)=(sinωx+acosωx)(a∈R,0<ω≤1)满足:f(x)=f(-x),f(x-π)=f(x+π).
(I)求f(x)的解析式;
(II)若m2-4n>0,m,n∈R,求证:“|m|+|n|<1”是“方程[f(x)]2+mf(x)+n=0在区间(-,)内有两个不等的实根”的充分不必要条件.
16、给出下列四个命题:①设 ,若
,若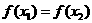
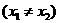 ,则
,则 ;②若偶函数
;②若偶函数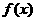 在
在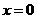 处可导,则
处可导,则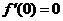 ; ③函数
; ③函数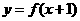 与
与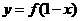 的图象关于直线
的图象关于直线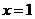 对称;④函数
对称;④函数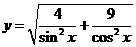 的最小值是 5.则其中错误的命题的序号是 .
的最小值是 5.则其中错误的命题的序号是 .
15、在R上定义运算 :x
:x y=x(1-y),若不等式(x-a)
y=x(1-y),若不等式(x-a)  (x+a)<1对任意实数x恒成立,则实数a的取值范围是
(x+a)<1对任意实数x恒成立,则实数a的取值范围是
14、平面内有n个圆两两相交,任何三个圆不过同一点,写出交点个数随着n的变化而变化的函数关系式f(n):_________________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com