22. (本大题满分14分)如图，曲线段OMB是函数f (x) = x² (0＜x＜6)的图象，BA⊥x轴于A，曲线段OMB上一点M (t，t ² )处的切线PQ交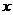轴于点P，交线段AB于点Q． 　　 (1)试用t表示切线PQ的方程； 　　 (2)设△QAP的面积为g (t)，若函数g (t)在(m，n)上单调递减，试求出m的最小值； 　　 (3)求函数g (t)的值域．

21. (本大题满分12分)已知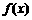是定义在R上的不恒为0的函数，且对于任意a、b∈R都满足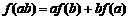：． 　　 (1)求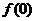、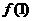的值； 　　 (2)判断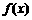的奇偶性并证明你的结论； 　　 (3)若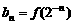， (n＞0，n∈N)，求数列{b_n}的前n项和．

20. (本大题满分12分)从4月1日开始，有一新款服装投入某商场销售，4月1日该款服装销售出20件，第二天销售出25件，第三天销售出40件，以后，每天售出的件数分别递增15件，直到4月12号日销售量达到最大，然后，每天销售的件数分别递减10件． 　　 (1)记该款服装四月份日销售量与销售天数n的关系为a_n，求a_n； 　　 (2)求四月份的总销售量； 　　 (3)按规律，当该商场销售此服装超过1 300件时，社会上就流行，而日销售量连续下降，且日销售量低于100件时，则流行消失，问：该款服装在社会上流行是否超过10天？说明理由．

19. 　(本大题满分12分)数列{a_n}的前n项和为S_n，已知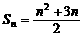． 　　 (1)求数列{a_n}的通项公式； 　　 (2)若数列{c_n}满足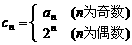，数列{c_n}的前n项和为T_n，当n为偶数时，求T_n； 　(3)张三同学利用第(2)题中的T_n设计了一个程序流程如图，但李四同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去，而无法结束)．你是否同意李四同学的观点？请说明理由．

18. (本大题满分12分)已知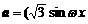，1)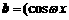，，0)，其中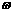＞0，又函数f (x) 是以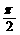为最小正周期的周期函数，当x∈[0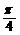，]时，函数f (x)的最小值为－2． 　　 (1)求f (x)的解析式； 　　 (2)写出函数f (x)的单调递增区间； 　　 (3)将函数f (x)的图象沿向量m平移后可以得到一个偶函数的图象，请写出一个符合条件的向量m．

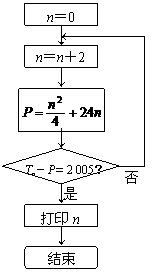
17. (本大题满分12分)已知关于x的不等式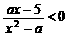的解集为M． 　　 (1)当a = 4时，求集合M； 　　 (2)若3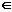M且5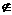M，求实数a的取值范围．

16. 已知函数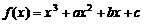，[-2，2]表示的曲线过原点，且在x = ±1处的切线斜率均为－1，则f (x)的解析式为f (x) = 　▲　．

15. 函数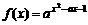在区间(1，+∞)上是单调增函数，则a的取值范围是　▲　．

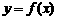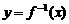14. 函数图象恒过定点(0，1)，若存在反函数，则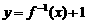的图象必过定点　▲　．

13. 已知集合P = {(x，y)｜y = m}，Q = {(x，y)｜y = ，a＞0，a≠1}，如果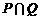有且只有一个元素，那么实数m的取值范围是　▲　．