
题目列表(包括答案和解析)
6.设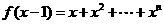 ,且
,且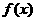 的展开式中所有项的系数和为
的展开式中所有项的系数和为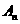 ,则
,则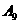 的值为( )
的值为( )
A.514 B.1026 C. 510 D. 1022
5.函数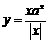
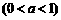 的图象的大致形状是 ( )
的图象的大致形状是 ( )
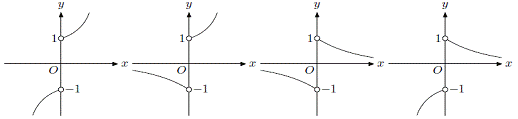
A. B. C. D.
4.在平面上,已知点A(2,1),B(0,2),C(-2,1),O(0,0).给出下面的结论:
①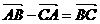 ②
②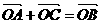 ③
③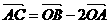
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.0个
3.数列{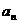 }的前n项和
}的前n项和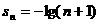 ,则
,则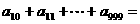 ( )
( )
A.2 B.-2 C.3 D.-3
2.若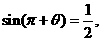 则
则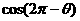 等于( )
A.
等于( )
A.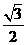 B.-
B.- 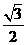 C.
C.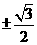 D.
D.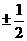
1.设集合A和集合B都是实数集R,映射f:A→B使集合A中的元素x与集合B中的元素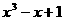 对应,则在映射f下,象1的原象所成的集合是( )
对应,则在映射f下,象1的原象所成的集合是( )
A.{1} B.{0} C.{0,1,-1} D.{0,-1,-2}
22.(本小题满分14分)
设 的图象上任意两点,且
的图象上任意两点,且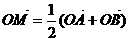 ,已知点M的横坐标为
,已知点M的横坐标为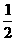 .
.
(I)求证:M点的纵坐标为定值;
(Ⅱ)若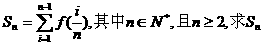 ;
;
(Ⅲ)已知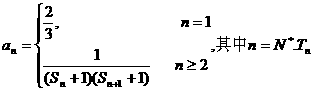 为数列
为数列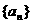 的前n项和,若
的前n项和,若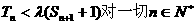 都成立,试求
都成立,试求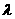 的取值范围.
的取值范围.
21.(本小题满分12分)
双曲线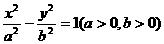 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为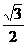 ,其中A(0,-b),B(a,0).
,其中A(0,-b),B(a,0).
(I)求双曲线的标准方程;
(Ⅱ)设F是双曲线的右焦点,直线l过点F且与双曲线的右支交于不同的两点P、Q,点M为线段PQ的中点. 若点M在直线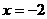 上的射影为N,满足
上的射影为N,满足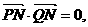
且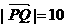 ,求直线l的方程.
,求直线l的方程.
20.(本小题满分12分)
设函数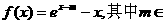 R.
R.
(I)求函数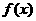 的最值;
的最值;
(Ⅱ)给出定理:如果函数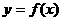 在区间[
在区间[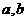 ]上连续,并且有
]上连续,并且有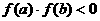 ,那么,函数
,那么,函数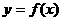 在区间
在区间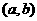 内有零点,即存在
内有零点,即存在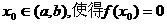 .
.
运用上述定理判断,当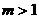 时,函数
时,函数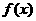 在区间
在区间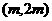 内是否存在零点.
内是否存在零点.
19.(本小题满分12分)
下表是某地一年中10天测量的白昼时间统计表(时间近似到0.1小时)
|
日期 |
1月1日 |
2月28 日 |
3月21 日 |
4月27 日 |
5月6 日 |
6月21 日 |
8月13 日 |
9月20 日 |
10月25日 |
12月21日 |
|
日期位置序号x |
1 |
59 |
80 |
117 |
126 |
172 |
225 |
263 |
298 |
355 |
|
白昼时间y(小时) |
5.6 |
10.2 |
12.4 |
16.4 |
17.3 |
19.4 |
16.4 |
12.4 |
8.5 |
5.4 |
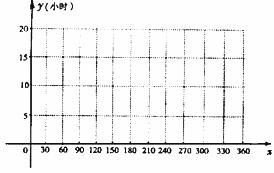
(I)以日期在365天中的位置序号x为横坐标,白昼时间y为纵坐标,在给定坐标系中画出这些数据的散点图;
(Ⅱ)试选用一个形如 的函数来近似描述一年中白昼时间y与日期位置序号x之间的函数关系.[注:①求出所选用的函数关系式;②一年按365天计算]
的函数来近似描述一年中白昼时间y与日期位置序号x之间的函数关系.[注:①求出所选用的函数关系式;②一年按365天计算]
(Ⅲ)用(Ⅱ)中的函数模型估计该地一年中大约有多少天白昼时间大于15.9小时.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com