
题目列表(包括答案和解析)
8.小芳和爸爸、妈妈三人玩跷跷板,三人的体重一共为150千克,爸爸坐在跷跷板的一端;体重只有妈妈一半的小芳和妈妈一同坐在跷跷板的另一端.这时,爸爸的那一端仍然着地.请你猜一猜小芳的体重应小于( )
A. 49千克 B. 50千克 C. 24千克 D. 25千克
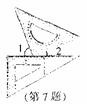
7. 一副三角扳按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为 ( )
A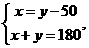 B
B 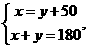 C
C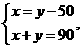 D
D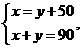
6.不等式组 的整数解的个数是 ( )
的整数解的个数是 ( )
 A.1个 B.2个 C.3个 D.4个
A.1个 B.2个 C.3个 D.4个
5.根据下图所示,对a、b、c 三种物体的重量判断正确的是( )
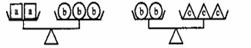 A.a<c
B. a<b C. a>c D. b<c
A.a<c
B. a<b C. a>c D. b<c
4.将方程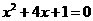 配方后,原方程变形为 ( )
配方后,原方程变形为 ( )
A.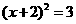 B.
B.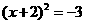 C.
C.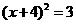 D.
D.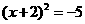
3.不等式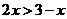 的解集是( )
的解集是( )
A.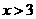 B.
B.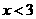 C.
C.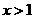 D.
D.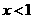
2.据温州市气象台“天气预报”报道,今天西部山区的最低气温是零下1 ℃,最高气温是6 ℃,则今天西部山区气温t(℃)的范围是( )
A. t >1 B.-1 <t<6 C.t<6 D.-1≤t≤6
1.如果 +2=0,那么“
+2=0,那么“ ”内应填的实数是 ( )
”内应填的实数是 ( )
A.-2 B.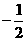 C.
C.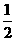 D.2
D.2
12. (本题14分)
(本题14分)
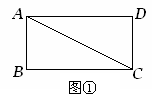
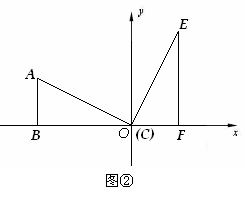
如图①,矩形ABCD被对角线AC分为两个直角三角形,AB=3,BC=6.现将Rt△ADC绕点C顺时针旋转90º,点A旋转后的位置为点E,点D旋转后的位置为点F.以C为原点,以BC所在直线为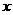 轴,以过点C垂直于BC的直线为
轴,以过点C垂直于BC的直线为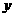 轴,建立如图②的平面直角坐标系.
轴,建立如图②的平面直角坐标系.
(1) 求直线AE的解析式;
(2) 将Rt△EFC沿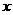 轴的负半轴平行移动,如图③.设OC=
轴的负半轴平行移动,如图③.设OC=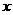 (
(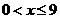 ),Rt△EFC与Rt△ABO的重叠部分面积为s;
),Rt△EFC与Rt△ABO的重叠部分面积为s;
①
当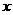 =1与
=1与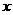 =8时,求s的值;
=8时,求s的值;
②
S是否存在最大值?若存在,求出这个最大值及此时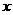 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.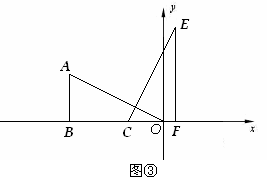
11. (本题10分)
小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图(1),垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
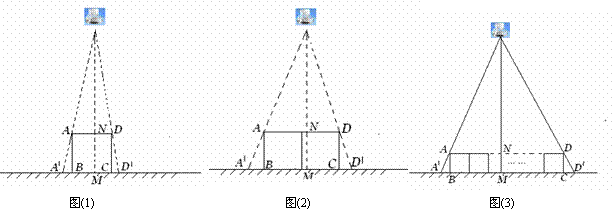
(2)不改变(1)中灯泡的高度,将两个边长为30cm的正方形框架按图(2)摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图(3)摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com