
题目列表(包括答案和解析)
2.右边几何体的主视图是( )
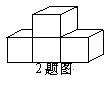

(A) (B) (C) (D)
1.2的算术平方根是( )
(A)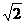 (B)-
(B)-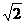 (C)±
(C)±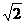 (D)2
(D)2
4.已知抛物线y=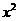 -5mx+4m2 (m为常数). (1)求证:此抛物线与x轴一定有交点;
-5mx+4m2 (m为常数). (1)求证:此抛物线与x轴一定有交点;
(2)是否存在正数m,使已知抛物线与x轴两个交点的距离等于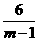 ?若存在,求出m的值;若不存在,说明理由.
?若存在,求出m的值;若不存在,说明理由.
3.已知矩形的长大于宽的2倍,周长为12,从它的一个顶点作一条射线,将矩形分成一个三角形和一个梯形,且这条射线与矩形一边所成的角的正切值等于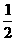 ,设梯形的面积为S,梯形中较短的底的长为x,试写出S与x的函数关系式,并求出自变量x的取值范围。
,设梯形的面积为S,梯形中较短的底的长为x,试写出S与x的函数关系式,并求出自变量x的取值范围。
2. 一次函数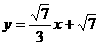 的图象分别与x轴、y轴交于A、B两点,点C(a,0)(a<0)使△ABC为等腰三角形,求经过B、C两点的一次函数的解析式。
的图象分别与x轴、y轴交于A、B两点,点C(a,0)(a<0)使△ABC为等腰三角形,求经过B、C两点的一次函数的解析式。
1.已知α、β是方程x2+x+a=0的两个实数根。求 a的取值范围;⑵试用a表示|α|+|β|。
3、某家庭装饰厨房需用480块某品牌的同一种规格的瓷砖,装饰材料商场出售的这种瓷砖有大、小两种包装,大包装每包50片,价格为30元;小包装每包30片,价格为20元,若大、小包装均不拆开零售,那么怎样制定购买方案才能使所付费用最少?
2、某商店销售甲、乙两种成衣,甲每件成衣进价10元,售价18元,乙每件进价8元,售价13元,且进价、售价始终不变,现准备购进甲、乙两种成衣共20件,所用资金不低于175元,不高于180元。问:(1)该商店有几种进货方案?
(2)该商店采用何种方案进货利润最大?最大利润是多少?
1、某工厂现有甲种原料226kg,乙种原料250kg,计划利用这两种原料生产A、B两种产品共40件,生产A、B两种产品用料情况如下表:
|
|
需要甲原料 |
需要乙原料 |
|
一件A产品 |
7kg |
4kg |
|
一件B产品 |
3kg |
10kg |
设生产A产品x件,请解答下列问题:
(1) 求x的值,再说明有哪几种符合题意的生产方案;
(2) 若甲种原料50元/kg,乙种原料40元/kg,说明(1)中哪种方案较优?
4、某学校组织高一学生到学农基地进行学农劳动,基地安排他们住宿的宿舍,如果每室安排住8人,则少12个床位;如果每室安排住9人,又空出2个房间,问:该学校参加这次学农的学生至少有多少人?基地安排给他们的宿舍至多有几间?
l 方案问题:
练习:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com