
题目列表(包括答案和解析)
2.请给出一元二次方程 =0的一个常数项,使这个方程有两个不相等的实数根。
=0的一个常数项,使这个方程有两个不相等的实数根。
1、 某市政府切实为残疾人办实事,在区道路改造中为盲人修建一条长3000m的盲道,根规 划设计和要求,该市工程队在实际施工时增加了施工人员,每天修建的盲道比原计划增加50%,结果提前2天完成,则实际每天修建盲道__________m.
4.某市为处理污水需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时每天比原计划多铺设10米,结果提前20天完成任务。设原计划每天铺设管道x米,则可得方程( )
 (A)
(A) (B)
(B)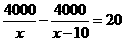
(C)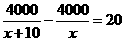 (D)
(D)
3。 某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
|
捐款(元) |
1 |
|
3 |
4 |
||
|
人 数 |
6 |
|
|
7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有 名同学,捐款3元的有
名同学,捐款3元的有 名同学,根据题意,可得方程组
名同学,根据题意,可得方程组
A、 B、
B、 C、
C、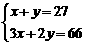 D、
D、
2、一元二次方程 的根的情况为( )
的根的情况为( )
A、有两个不相等的实数根 B、有两个相等的实数根
C、只有一个实数根 D、没有实数根
1. 已知直角三角形的两条直角边的长恰好是方程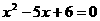 的两根,则此直角三角形的斜边长为( ).
的两根,则此直角三角形的斜边长为( ).
A.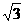 B.3 C.
B.3 C. D.13
D.13
22.(本题6分)问题:你能比较两个数20042005和20052004的大小吗?
 为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较nn+1和(n+1)n的大小(n是自然数),然后我们从分析n=1,n=2,n=3,…… 这些简单情形入手,从中发现规律,经过归纳,猜想出结论。
为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较nn+1和(n+1)n的大小(n是自然数),然后我们从分析n=1,n=2,n=3,…… 这些简单情形入手,从中发现规律,经过归纳,猜想出结论。
(1)通过计算,比较下列各组中两个数的大小:
① 12 21 ② 23 32 ③ 34 43
④ 45 54 ⑤ 56 65 ⑥ 67 76 ……
(2)从第(1)题的结果经过归纳,可以猜想出nn+1和(n+1)n的大小关系式是
(3)根据上面归纳猜想得到的一般结论,试比较两个数的大小:
20042005 20052004
21. (本题8分)如图,某长方形广场的四角都有一块半径相同的四分之一圆形的草地,若圆形的半径为r米,长方形的宽为a米,长为b米。
(本题8分)如图,某长方形广场的四角都有一块半径相同的四分之一圆形的草地,若圆形的半径为r米,长方形的宽为a米,长为b米。
(1)用代数式表示空地的面积;
(2)若长方形的宽为200米,长为250米,圆形的
半径为10米,求广场空地的面积。(π取3.14)
20. (本题6分)我市某水库受台风“海棠”影响,某天8﹕00的水位为-0.2m(以警戒线为基准,记高于警戒线的水位为正),在以后的6个时刻测得的水位升降情况如下(记上升为正,单位:m):0.4,-0.7,0.3,-0.3,-0.1,0.2.
经这6次水位升降后,水库的水位超过警戒线了吗?
19. (本题6分)据有关部门统计,2004年我区农民人均纯收入从2003年的8505元增加到9359元,增长的百分比是多少(精确到1%)?按这样的增长速度,2005年我区农民人均纯收入将达到多少(精确到1元)?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com